Datastruture: Tree

导言

When i learn the radix tree in mult-level page table, I was confused by various kinds of tree and thier names

Common tree structures

binary tree shape

• 满二叉树
  • 如果一棵二叉树的结点要么是叶子结点，要么它有两个子结点，这样的树就是满二叉树。
• 完全二叉树
  • 除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置

node store complete data

• 二叉搜索树（Binary Search Tree，BST）
  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉排序树
  • n个节点组成 二叉搜索树，由于满足递归关系 C(n) = \sum(C(i-1)*C(n-i)), 所以结果为卡塔兰数
• 平衡二叉搜索树（简称 平衡二叉树 AVL树（Adelson-Velsky and Landis）），（Balanced Binary Tree？）
  • 平衡二叉树属于搜索二叉树的一种。
  • 左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
  • 红黑树是一种二叉平衡搜索树，这两个树不是独立的，所以C++中map、multimap、set、multiset的底层实现机制是二叉平衡搜索树，再具体一点是红黑树。
• 赫夫曼树：
  • 当用 n 个结点（都做叶子结点且都有各自的权值）构建一棵树时，如果构建的这棵树的带权路径长度（WPL）最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。
  • 树的带权路径长度（WPL）：树中所有叶子结点的带权路径长度之和。
  • 结点的带权路径长度：指的是从根结点到该结点之间的路径长度(叶节点深度)与该结点的权的乘积。

Trie

In computer science, a trie (/ˈtriː/, /ˈtraɪ/), also called digital tree or prefix tree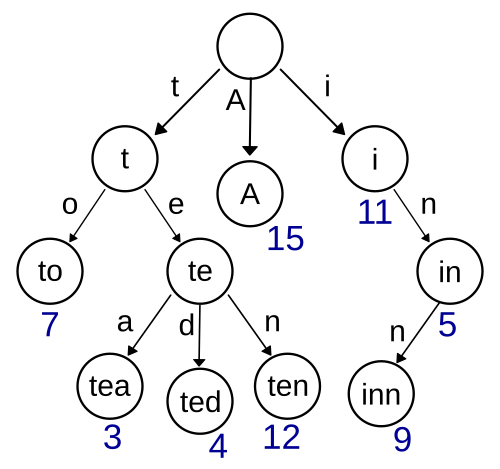

• is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set.
• These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters.
• In order to access a key (to recover its value, change it, or remove it), the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

Unlike a binary search tree

nodes in the trie do not store their associated key. Instead, a node's position in the trie defines the key with which it is associated. This distributes the value of each key across the data structure, and means that not every node necessarily has an associated value.

disadvantages of Trie and Radix tree

they can only be applied to strings of elements or elements with an efficiently reversible mapping to strings, they lack the full generality of balanced search trees, which apply to any data type with a total ordering.

radix tree

In computer science, a radix tree (also radix trie or compact prefix tree or compressed trie) is a data structure that represents a space-optimized trie (prefix tree)

• in which each node that is the only child is merged with its parent.
• The result is that the number of children of every internal node is at most the radix r of the radix tree, where r is a positive integer and a power x of 2, having x ≥ 1.

Unlike regular trees, edges can be labeled with (compressed)sequences of elements as well as single elements(1). This makes radix trees much more efficient for small sets (especially if the strings are long) and for sets of strings that share long prefixes.

1. elimination of branches of the nodes with a single child results in better in both space and time metrics.

Comparison to other data structures

Further more in wiki

radix tree in page table

TODO: ¹

参考文献

---

1. Variable Radix Page Table: A Page Table for Modern Architectures ↩

评论