Pytorch 2 ：Basic Conception & Dataset & Dataloader

导言

训练推理相关基本概念
数据集与数据加载器：学习如何使用torch.utils.data.Dataset和DataLoader来加载和处理数据。
数据预处理：介绍常用的数据预处理方法，如归一化、数据增强等。

什么是一“次”训练和推理？¶

在深度学习中，一次训练 或 一次推理 的范围取决于你关注的层次，主要有三种常见的粒度：

Inference（推理）：使用训练好的模型，在不计算梯度的情况下，对输入数据进行前向传播，得到输出结果。
Iteration（迭代）：一次前向传播 + 计算损失 + 反向传播 + 更新参数，处理 一个 batch 的数据。
Epoch（轮次）：遍历整个数据集一次，即所有 batch 都被处理了一遍。

推理（Inference）¶

推理就是使用训练好的模型进行前向传播，但 不需要计算梯度，也不更新参数，通常用于测试或实际应用中。例如：

with torch.no_grad():  # 关闭梯度计算，加速推理
    outputs = model(test_data)  # 只进行前向传播

推理时，batch size 也决定了一次推理处理多少样本。

Iteration（迭代）¶

当我们训练一个神经网络时，一般不会直接在整个数据集上进行计算，而是将数据集拆分成多个 batch，然后逐个 batch 送入模型进行训练。

一次迭代指的是：

取出一个 batch（批量）数据 送入神经网络。
前向传播（Forward Pass）：计算模型输出。
计算损失（Loss）。
反向传播（Backward Pass）：计算梯度。
更新参数（Optimizer Step）。

例如

for batch_data, batch_labels in dataloader:  # dataloader 按 batch 迭代数据
    optimizer.zero_grad()  # 清空梯度
    outputs = model(batch_data)  # 前向传播
    loss = loss_fn(outputs, batch_labels)  # 计算损失
    loss.backward()  # 反向传播
    optimizer.step()  # 更新参数

每次 for 循环的执行就是 一次迭代（Iteration），处理的是 一个 batch 的数据。

如果你的数据集有 1000 个样本，batch size=32，那么：

训练完整个数据集需要 1000/32 = 32 次 iteration（迭代）。
每次 iteration 仅处理 32 个样本，而不是整个数据集。

Epoch（轮次）¶

一次 epoch 指的是 整个数据集都被训练一次，也就是说 所有 batch 都被训练过一遍。

假设你的数据集有 1000 个样本，batch size = 32，
需要 1000 / 32 = 32 次 iteration 才能遍历完整个数据集，即完成 1 个 epoch。
如果训练 10 轮（epochs=10），则总共会进行 32 × 10 = 320 次 iteration。

代码示例：

epochs = 10  # 训练 10 轮
for epoch in range(epochs):
    for batch_data, batch_labels in dataloader:  # 每个 batch 训练一次
        optimizer.zero_grad()
        outputs = model(batch_data)
        loss = loss_fn(outputs, batch_labels)
        loss.backward()
        optimizer.step()

这个代码 完整遍历数据集 10 次，即 10 个 epoch，总共会执行 iteration = (数据集大小 / batch_size) × epochs。

多个 epoch 的必要性¶

一次 epoch 确实遍历了整个数据集，但它 并不意味着模型已经学好了。在深度学习中，我们通常需要多个 epoch 来让模型逐步优化，找到更好的参数。

1. 训练神经网络的本质¶

神经网络的训练本质上是一个优化问题，目标是找到一组最优的参数，使得模型的损失函数最小（即预测尽可能准确）。
训练的过程类似于爬山，我们需要沿着损失函数的梯度下降，不断调整模型参数，逐渐收敛到最优解。

如果只进行 1 个 epoch，那么：

参数更新次数较少，模型可能还没有足够的训练，误差仍然很大。
梯度下降未收敛，即模型还没有达到最优状态。
模型可能无法充分学习数据特征，导致性能较差。

因此，我们需要多次遍历数据集（多个 epoch），不断优化参数，使模型的表现更好。

2. 为什么一次 epoch 不够？¶

假设你的数据集有 10,000 个样本，batch size = 32，那么 1 个 epoch 需要 10,000 / 32 ≈ 312 次 iteration。

但在实际情况中：

神经网络一开始参数是随机的，它需要多个 epoch 来逐步学习数据中的模式。
优化算法（如梯度下降）不会在一次遍历后立即找到最优解，而是通过不断迭代找到更好的参数。
损失函数（Loss）下降的趋势通常是逐步收敛的，如下图所示：

Loss
↑
|      __
|    /    
|  /      
|/________  (多次 epoch 后收敛)
---------------->  Epoch

可以看到，在多个 epoch 之后，损失才会下降并趋于稳定。

3. 训练多个 epoch 会发生什么？¶

假设你训练 10 个 epoch，每个 epoch 的损失可能如下： | Epoch | Training Loss | |--------|-------------| | 1 | 1.2 | | 2 | 0.9 | | 3 | 0.7 | | 4 | 0.5 | | 5 | 0.4 | | ... | ... | | 10 | 0.2 |

可以看到，损失在逐渐降低，模型在逐步学习数据模式。如果只训练 1 个 epoch，损失可能仍然较高，模型的预测能力较弱。

4. 什么时候停止训练？¶

一般来说，你不会一直增加 epoch，因为： 1. 太少的 epoch → 欠拟合（Underfitting），模型还没学会数据中的模式。 2. 太多的 epoch → 过拟合（Overfitting），模型在训练集上效果很好，但在测试集上表现变差。

早停（Early Stopping）¶

常见的做法是：

监控验证集（Validation Set）的损失，如果发现连续几轮损失不再下降，就提前停止训练。
例如：

import torch
import torch.nn as nn
import torch.optim as optim

model = ...  # 定义模型
loss_fn = nn.CrossEntropyLoss()  # 损失函数
optimizer = optim.Adam(model.parameters(), lr=0.001)  # 优化器

best_val_loss = float('inf')  # 记录最小的验证损失
patience = 3  # 如果验证损失连续 3 次没有下降，则停止训练
counter = 0

for epoch in range(50):  # 最多训练 50 个 epoch
    train_loss = train_one_epoch(model)  # 训练一个 epoch
    val_loss = validate(model)  # 计算验证集损失

    if val_loss < best_val_loss:
        best_val_loss = val_loss
        counter = 0  # 重新计数
    else:
        counter += 1
        if counter >= patience:
            print(f"Early stopping at epoch {epoch}")
            break  # 提前停止训练

Batch size¶

batch size（批大小） 指的是 一次训练或推理时输入到神经网络中的样本数量。

Mini-batch

Mini-batch：小批量数据，介于批量梯度下降（全数据）和随机梯度下降（单样本）之间的折中方案。

为什么需要 batch size？¶

在深度学习中，训练神经网络时，我们通常不会一次性把所有数据都输入，而是分批（batch）输入。这样做的原因包括：

计算资源限制：一次性处理整个数据集可能会超出 GPU/CPU 的内存，而分批次处理可以减少内存占用。
加速训练：小批量数据可以在 GPU 上并行计算，提高效率。
更稳定的梯度下降：批量梯度下降（mini-batch gradient descent）可以在计算梯度时减少单个样本带来的噪声，使优化过程更加稳定。

Batch size 的不同取值影响¶

小 batch size（如 8, 16）
内存占用小，适用于小显存设备（如笔记本 GPU）。
噪声较大，梯度更新不稳定，但可能有助于泛化能力（即模型在未见过的数据上表现更好）。

大 batch size（如 128, 256, 1024）
计算效率高，但需要较大显存。
梯度更新更平稳，适用于大规模数据集。

代码示例

假设我们有一个数据集，并用 PyTorch 的 DataLoader 来加载数据：

import torch
from torch.utils.data import DataLoader, TensorDataset

# 假设我们有 1000 个样本，每个样本有 10 个特征
data = torch.randn(1000, 10)  # 1000 个样本，10 维特征
labels = torch.randint(0, 2, (1000,))  # 1000 个 0/1 标签

# 创建数据集
dataset = TensorDataset(data, labels)

# 设置 batch size = 32
batch_size = 32
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

# 迭代 DataLoader
for batch_data, batch_labels in dataloader:
    print(f"Batch shape: {batch_data.shape}")  # 输出 batch 大小
    break  # 只看第一个 batch

如果 batch_size=32，那么 dataloader 每次会返回 32 个样本，直到数据集遍历完。

BatchNorm¶

Batch Normalization（简称 BatchNorm）是一种加速神经网络训练的方法，它通过对每个 batch 内的数据进行归一化，使网络更稳定、更容易训练，并减少对超参数（如学习率、权重初始化等）的敏感性。

简单来说，BatchNorm 通过在每一层对数据进行归一化，使得数据分布更加平稳，避免梯度消失或梯度爆炸。

BN层只是效果会变好，因为感受到了细节。不是有batch就一定有BN层的意思。

核心思想¶

在深度神经网络中，数据流经每一层时，其分布可能会发生剧烈变化，导致训练变得困难（称为内部协变量偏移 Internal Covariate Shift）。BatchNorm 通过在每一层对输入数据进行标准化（归一化），让数据保持稳定的均值和方差，从而加速训练。

BatchNorm 公式

对于某一层的输入 x，我们计算它在当前 batch 内的均值和方差：

\[ \mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i $$ $$ \sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2 \]

然后对 x 进行归一化：

\[ \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \]

其中 ε 是一个很小的数，防止除零错误。

最后，BatchNorm 引入可学习参数 γ（缩放）和 β（平移）：

\[ y_i = \gamma \hat{x}_i + \beta \]

这使得网络即使在归一化之后，仍然可以恢复原始的特性表示能力。

BatchNorm 和 Batch Size 的关系¶

BatchNorm 的计算基于 当前 batch 内的均值和方差，因此Batch Size 直接影响 BatchNorm 的效果：

Batch Size 大（如 128，256）
计算的均值和方差更加稳定，因为 batch 内样本多，统计量准确。
训练更稳定，BatchNorm 能有效加速训练。
Batch Size 小（如 2，4，8）
Batch 内样本少，均值和方差的计算误差大，导致 BatchNorm 不稳定。
可能需要使用 Group Normalization（GN） 或 Layer Normalization（LN） 作为替代方案。

一般来说，BatchNorm 需要 batch size 至少大于 16 或 32 才能较好地工作。如果 Batch Size 太小（如 2~8），BatchNorm 可能会导致梯度不稳定，此时可以考虑：

使用 LayerNorm 或 GroupNorm，它们不依赖 batch 统计量。
使用 BatchNorm 的 running statistics（即 track_running_stats=True）。
使用 SyncBatchNorm（跨多个 GPU 计算 batch 统计量）。

代码示例

在 PyTorch 中，你可以使用 nn.BatchNorm1d（1D 数据，如全连接层）、nn.BatchNorm2d（2D 数据，如 CNN）、nn.BatchNorm3d（3D 数据，如 3D 卷积）。

import torch
import torch.nn as nn

# 定义一个带有 BatchNorm 的网络
class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()
        self.fc = nn.Linear(10, 20)
        self.bn = nn.BatchNorm1d(20)  # 1D 全连接层的 BatchNorm
        self.relu = nn.ReLU()

    def forward(self, x):
        x = self.fc(x)
        x = self.bn(x)  # 归一化
        x = self.relu(x)
        return x

# 测试
model = MyModel()
x = torch.randn(32, 10)  # Batch Size = 32
output = model(x)
print(output.shape)  # 输出: torch.Size([32, 20])

多通道¶

一般是任务特征很多维度时，拓展描述参数用的。参考教程。

比如：图像一般包含三个通道/三种原色（红色、绿色和蓝色）。实际上，图像不是二维张量，而是一个由高度、宽度和颜色组成的三维张量。所以第三维通过通道表示。

多通道举例说明

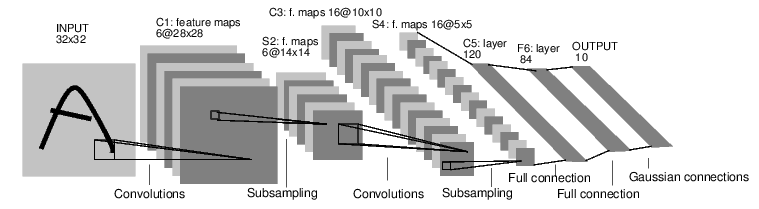
self.conv1 = nn.Conv2d(1, 6, 5) # 输入通道1，输出通道6，卷积核 5*5

如上图Input到C1，初始1通道变6通道，意味着对初始的A数据，有6个初始值不同的5*5卷积核操作，产生6张图。需要参数6*5*5。而长宽变化如下：

\[ 28=32-5+1 \]

如上图S2到C3, 6通道变16通道，相当于将6通道变1通道，重复16次。
6通道变1通道，通过6张图与由6个5*5卷积核组成的卷积核组作用，生成6张图，然后简单相加，变成1张。需要总参数16*6*5*5*5。
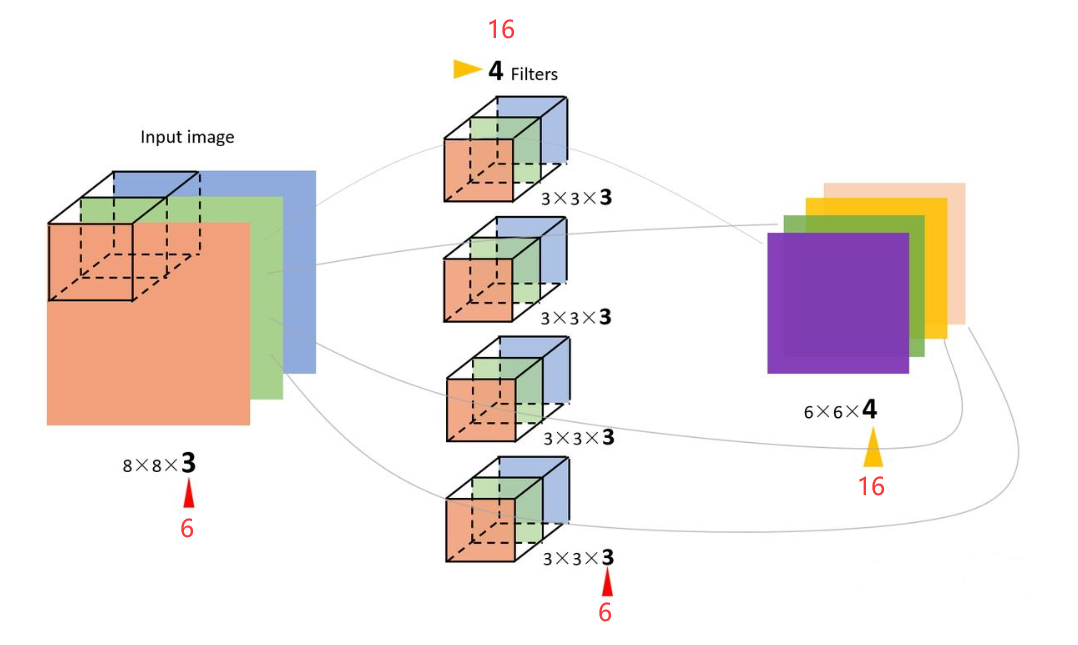
原理类似下图某些数据变成6和16：

梯度范数（Gradient Norm）¶

梯度范数（Gradient Norm）是深度学习中用于衡量模型参数更新方向与幅度的关键指标，其计算方式为所有参数梯度的平方和的平方根。这一指标在模型训练中具有以下核心作用：

1. 数学定义与计算¶

梯度范数的数学表达式为： [ G_{\text{norm}} = \sqrt{\sum_i \left( \frac{\partial L}{\partial \theta_i} \right)^2} ] 其中 $L$ 是损失函数，$\theta_i$ 表示模型参数。它通过整合所有参数的梯度信息，量化了当前参数更新方向的整体强度。

物理意义：梯度范数越大，表示参数更新幅度越大，可能接近陡峭的优化区域；反之则可能处于平坦区域或收敛状态。

2. 训练动态监测¶

梯度范数是诊断训练问题的核心指标：

梯度爆炸：若梯度范数急剧增长（如指数级），表明参数更新幅度过大，可能导致模型震荡或发散。
梯度消失：若梯度范数趋近于零，表明反向传播信号微弱，模型可能无法有效更新参数。
合理范围：理想情况下，梯度范数应平稳下降，反映模型逐步收敛到稳定解。

案例：在Transformer模型中，梯度范数的异常波动常与层归一化（LayerNorm）位置（Pre-Norm vs Post-Norm）相关。Post-Norm结构因梯度累积更易出现爆炸，需结合Warmup策略平衡。

3. 模型检查点选择策略¶

用户提到的“梯度范数峰值后选择检查点”是一种动态筛选方法，其原理如下：

峰值检测：梯度范数达到峰值时，通常对应训练初期参数快速调整阶段，此时模型可能处于不稳定状态。
收敛判断：峰值后梯度范数与损失函数同步下降，表明模型进入平缓收敛区（Flat Minimum Region），泛化能力更强。
稳定性验证：需同时满足：
梯度范数连续多步下降（如波动幅度<3%）；
损失值低于预训练基准线（如预训练损失的95%）。

优势：相比固定周期保存，该方法可过滤噪声干扰，提升生成结果的稳定性（如减少视频生成中的伪影）。

4. 在多任务学习中的扩展应用¶

梯度范数还可用于动态平衡多任务训练的权重：

GradNorm算法：通过约束不同任务梯度范数的相对大小，使各任务以相近速度收敛。例如，在推荐系统中，点击率（CTR）和转化率（CVR）任务的梯度范数差异过大会导致模型偏向主导任务，而GradNorm可自动调整损失权重。
实现效果：实验表明，该方法可使多任务模型的AUC方差降低70%，线上指标提升3-4%。

5. 与其他技术的关联¶

优化器设计：Adam等自适应优化器内部隐式依赖梯度范数调整学习率，但显式监控可辅助超参数调优。
归一化技术：LayerNorm和RMSNorm通过控制激活值分布间接影响梯度范数，Pre-Norm结构因梯度路径更短，更易维持合理梯度范数范围。

总结¶

梯度范数不仅是训练过程的“健康指标”，还可作为主动优化工具。通过动态监测其变化，开发者能更精准地控制模型收敛方向，尤其在生成式模型（如视频生成）和多任务场景中，这一指标对提升稳定性具有关键意义。