AMD Architecture on EPYC
ROMA SOC架构
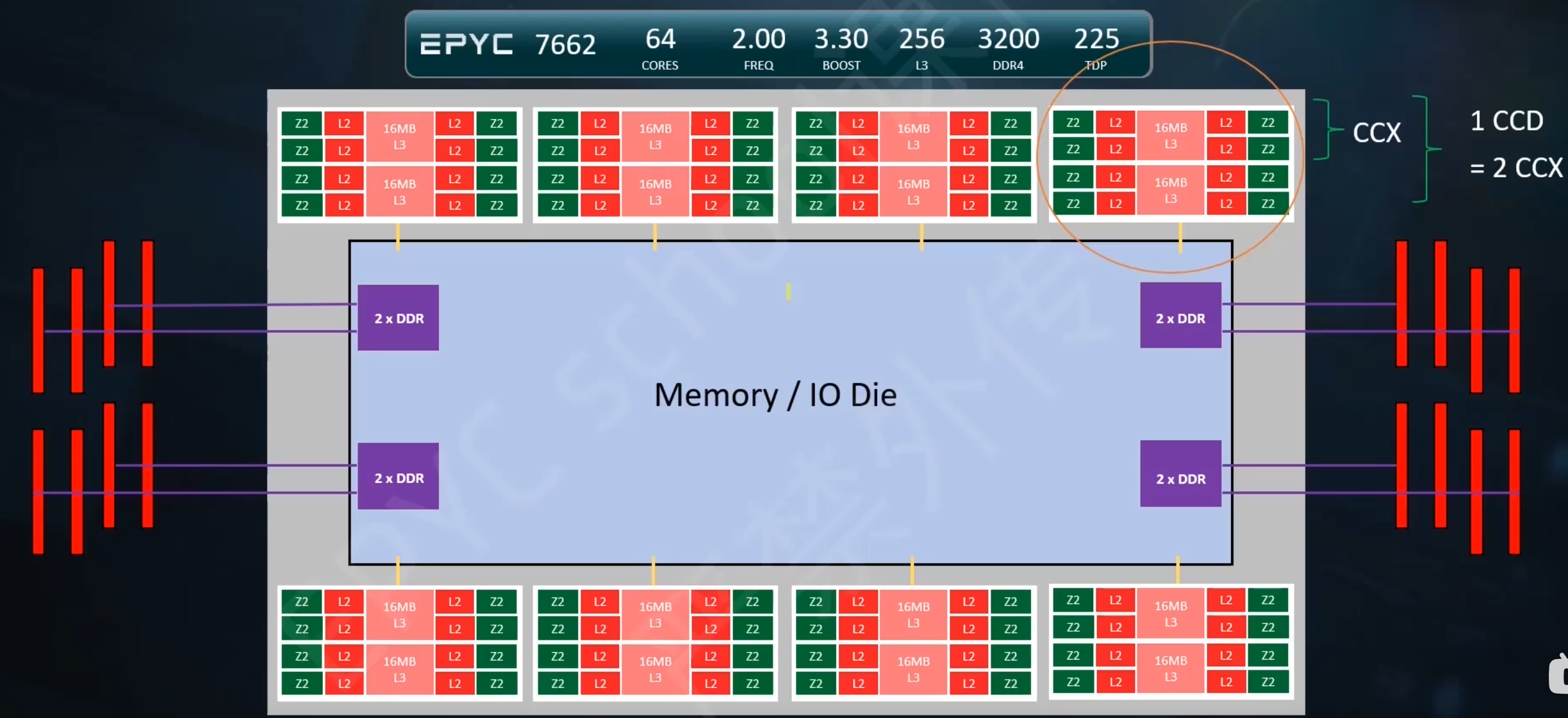
基本概念
CCD CCX
ROMA与MILAN架构比较
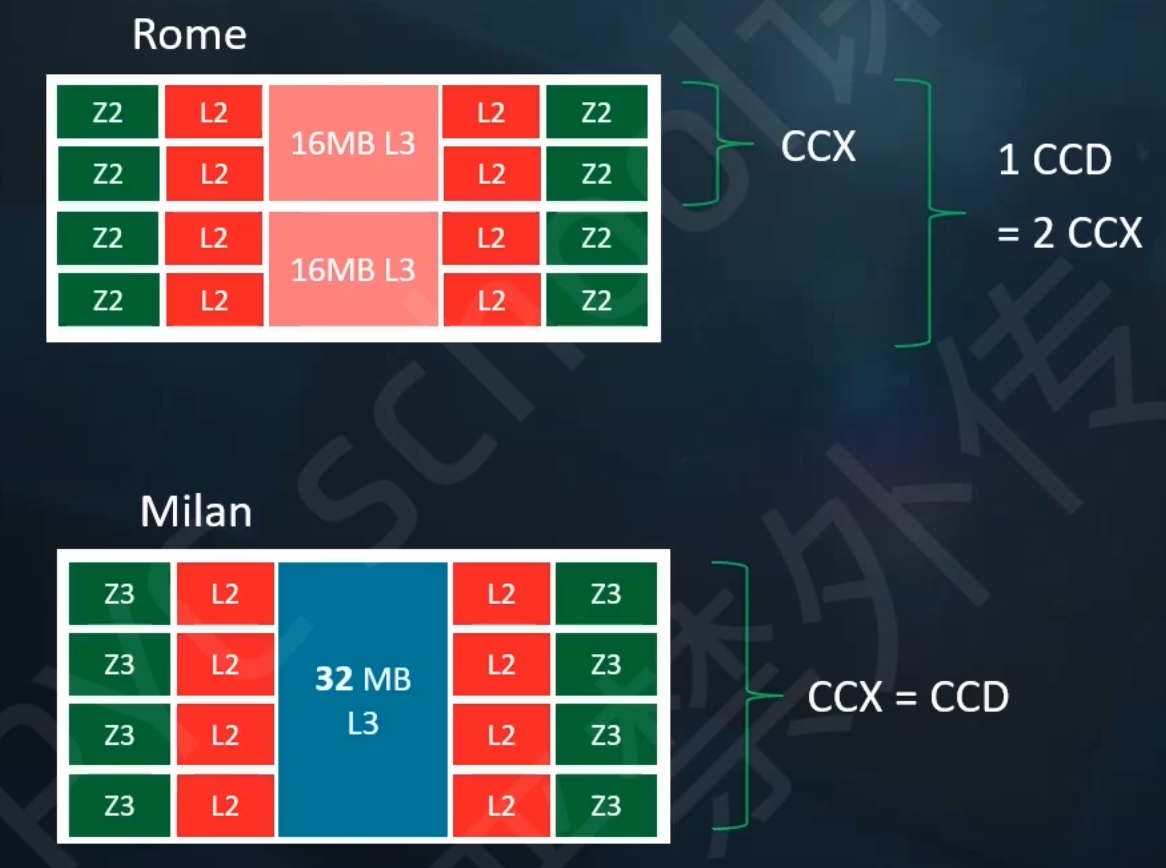
Roma使用Zen2核心,MILan使用Zen3核心。而且后者缓存更大,核心通信延迟更低。
计算CCD和CCX
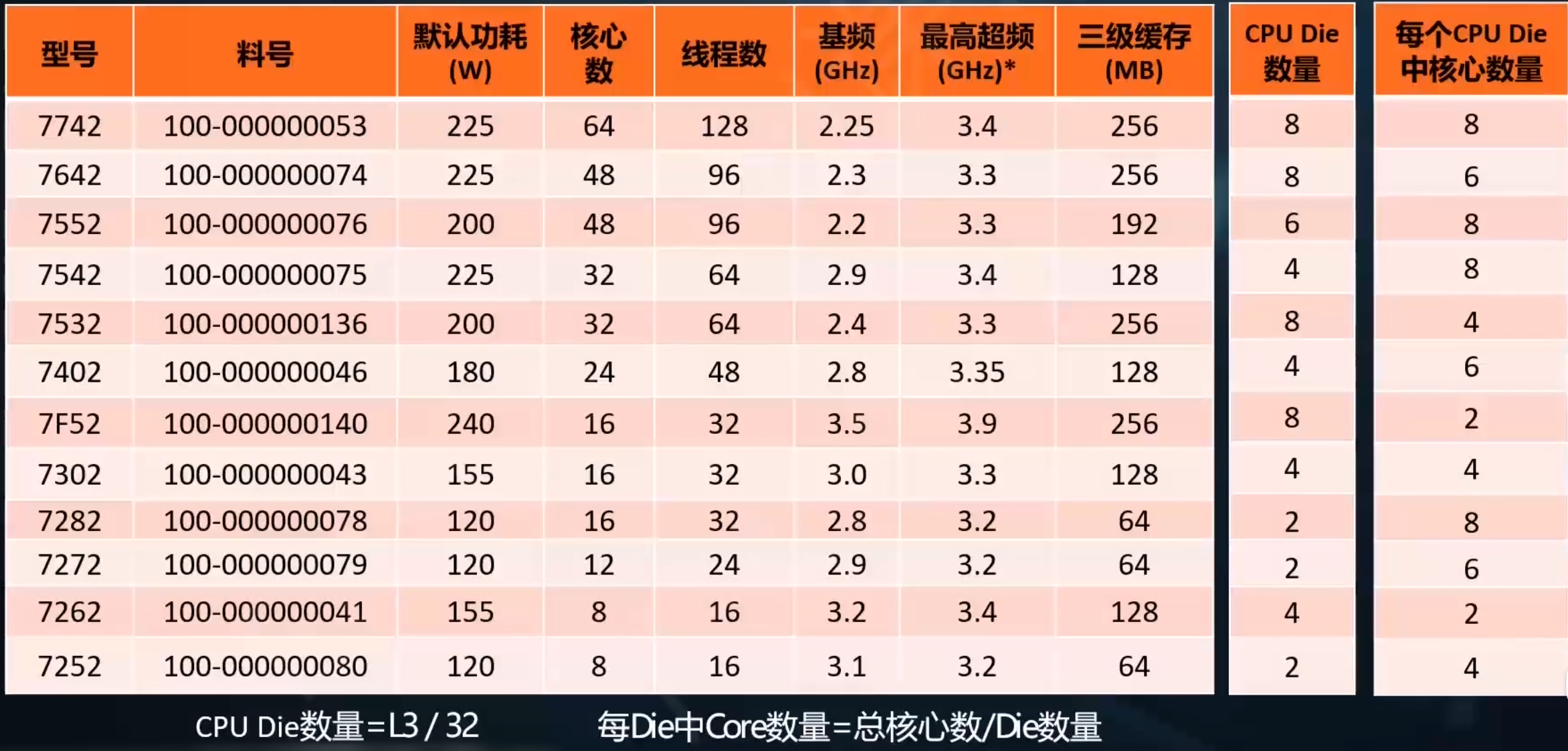
需要进一步的研究学习
暂无
遇到的问题
暂无
开题缘由、总结、反思、吐槽~~
参考文献
无

CCD CCX

Roma使用Zen2核心,MILan使用Zen3核心。而且后者缓存更大,核心通信延迟更低。

暂无
暂无
无
https://community.arm.com/arm-community-blogs/b/operating-systems-blog/posts/arm-neon-programming-quick-reference
暂无
暂无
https://blog.csdn.net/heliangbin87/article/details/79581113?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1.no_search_link&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1.no_search_link
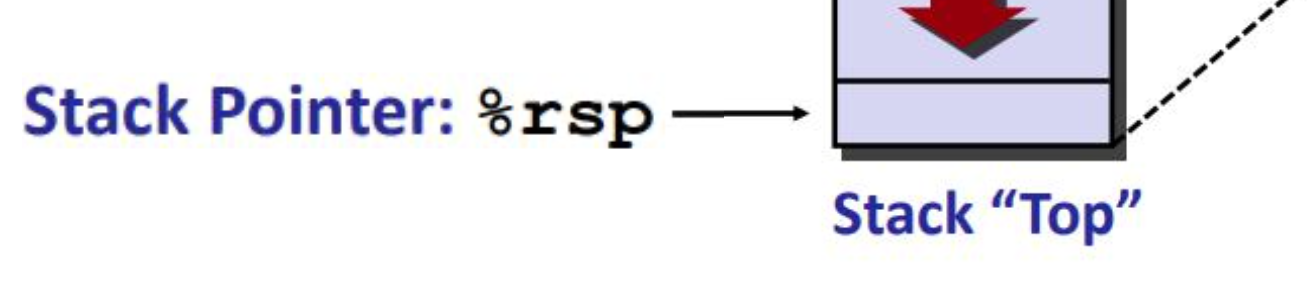
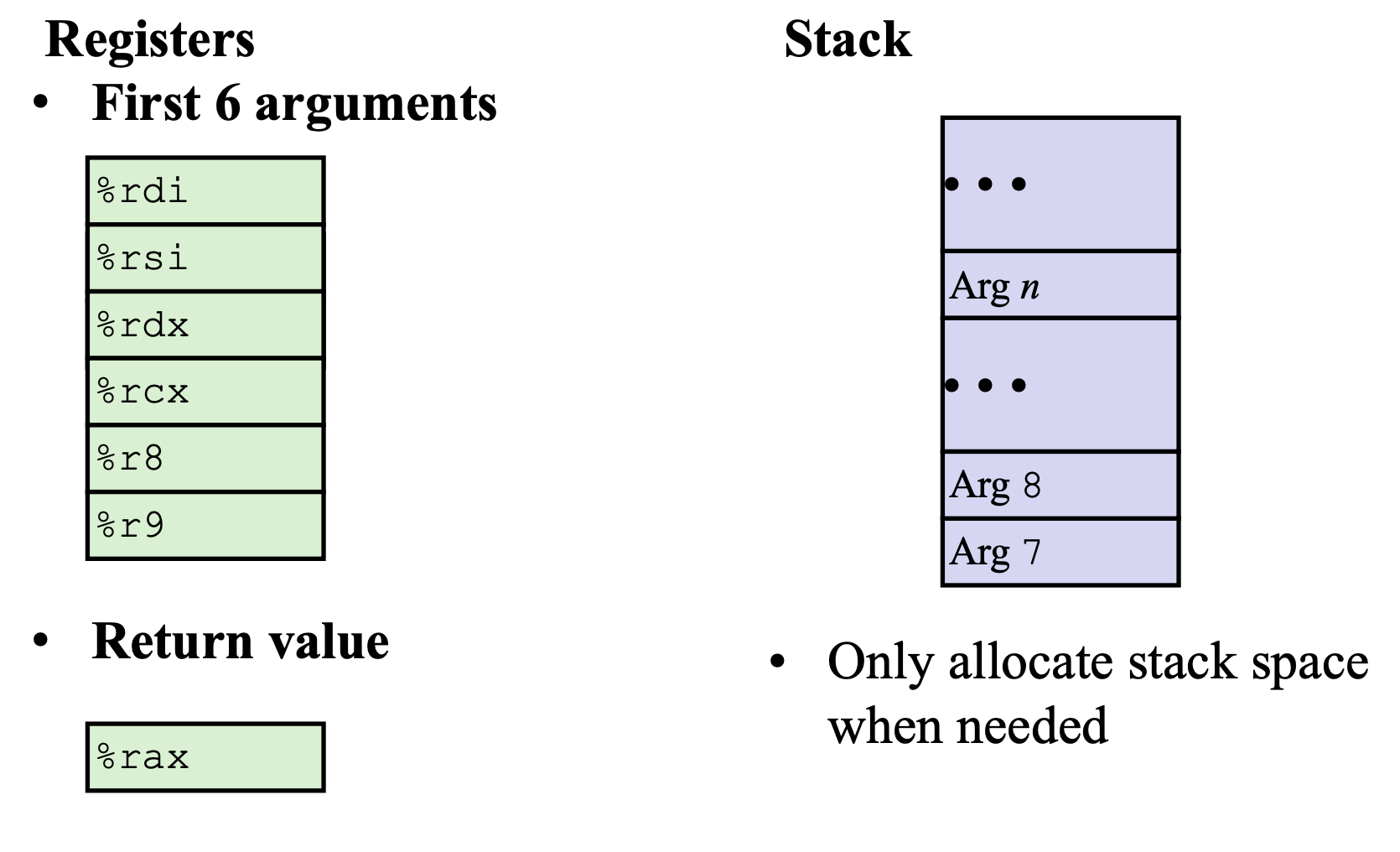
caller 调用者 callee 被调用者
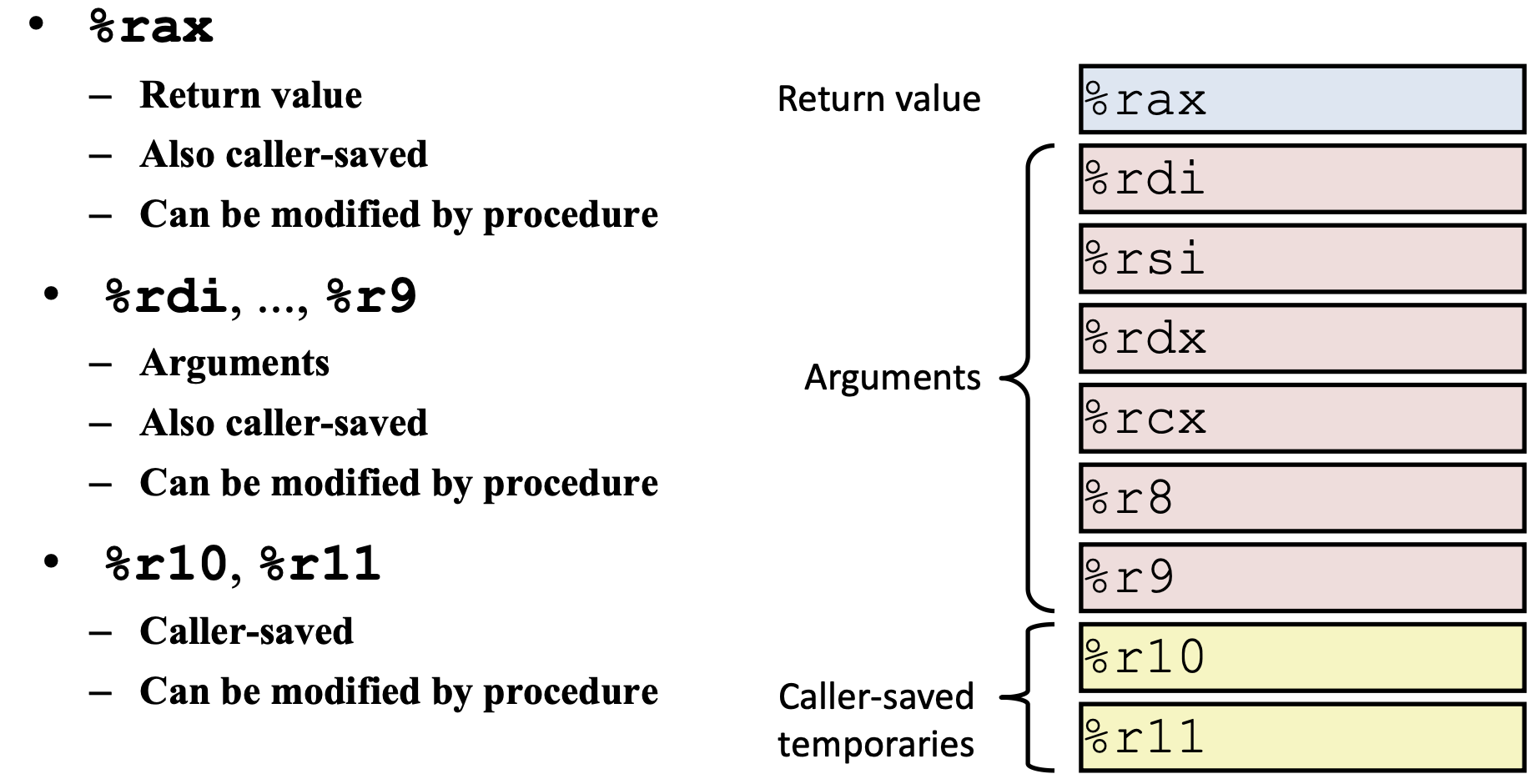
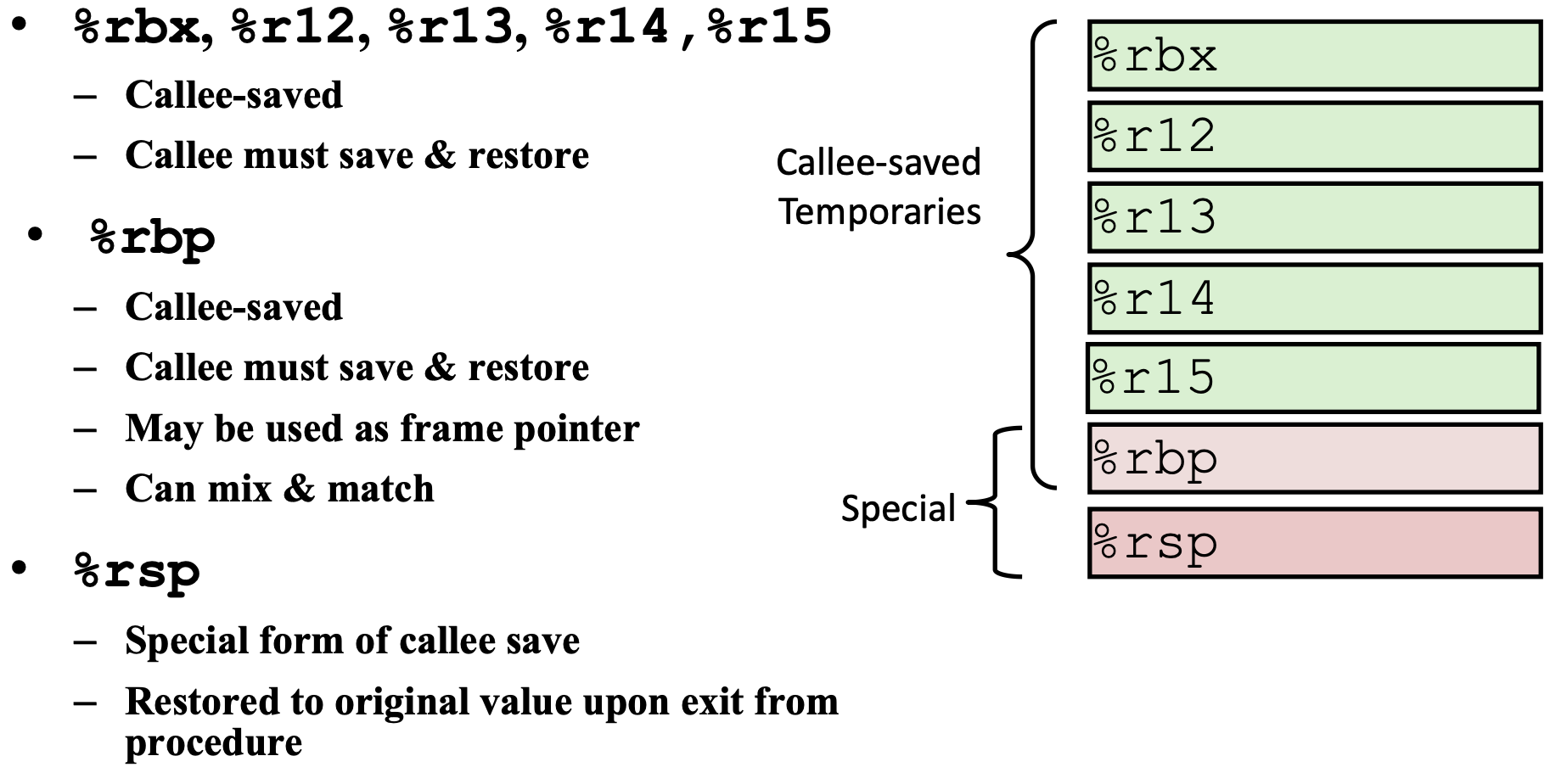
https://bkfish.github.io/2018/12/21/CSAPP又双叒叕来一遍之函数调用过程栈帧的变化/

暂无
暂无
无
SIMD全称Single Instruction Multiple Data,单指令多数据流,能够复制多个操作数,并把它们打包在大型寄存器的一组指令集。
通过使用矢量寄存器,指令译码后几个执行部件同时访问内存,一次性获得所有操作数进行运算。这个特点使SIMD特别适合于多媒体应用等数据密集型运算。如 AMD的3D NOW!技术
MMX是由57条指令组成的SIMD多媒体指令集,MMX将64位寄存当作2个32位或8个8位寄存器来用,只能处理整形计算,这样的64位寄存器有8组,分别命名为MM0~MM7.这些寄存器不是为MMX单独设置的,而是借用的FPU的寄存器,占用浮点寄存器进行运算(64位MMX寄存器实际上就是浮点数寄存器的别名),以至于MMX指令和浮点数操作不能同时工作。为了减少在MMX和浮点数模式切换之间所消耗的时间,程序员们尽可能减少模式切换的次数,也就是说,这两种操作在应用上是互斥的。
SSE为Streaming SIMD Extensions的缩写。Intel SSE指令通过128bit位宽的专用寄存器, 支持一次操作128bit数据. float是单精度浮点数, 占32bit, 那么可以使用一条SSE指令一次计算4个float数。注意这些SSE指令要求参数中的内存地址必须对齐于16字节边界。
SSE有8个128位寄存器,XMM0 ~XMM7。此外SSE还提供了新的控制/状态寄存器MXCSR。为了回答这个问题,我们需要了解CPU的架构。每个core是独占register的

addps xmm0, xmm1 ; reg-reg addps xmm0, [ebx] ; reg-mem sse提供了两个版本的指令,其一以后缀ps结尾,这组指令对打包单精度浮点值执行类似mmx操作运算,而第二种后缀ss
 1. SSE2则进一步支持双精度浮点数,由于寄存器长度没有变长,所以只能支持2个双精度浮点计算或是4个单精度浮点计算.另外,它在这组寄存器上实现了整型计算,从而代替了MMX.
2. SSE3支持一些更加复杂的算术计算.
3. SSE4增加了更多指令,并且在数据搬移上下了一番工夫,支持不对齐的数据搬移,增加了super shuffle引擎.
4. 由于2007年8月,AMD抢先宣布了SSE5指令集。之后Intel将新出的叫做AVX指令集。由于SSE5和AVX指令集功能类似,并且AVX包含更多的优秀特性,因此AMD决定支持AVX指令集
1. SSE2则进一步支持双精度浮点数,由于寄存器长度没有变长,所以只能支持2个双精度浮点计算或是4个单精度浮点计算.另外,它在这组寄存器上实现了整型计算,从而代替了MMX.
2. SSE3支持一些更加复杂的算术计算.
3. SSE4增加了更多指令,并且在数据搬移上下了一番工夫,支持不对齐的数据搬移,增加了super shuffle引擎.
4. 由于2007年8月,AMD抢先宣布了SSE5指令集。之后Intel将新出的叫做AVX指令集。由于SSE5和AVX指令集功能类似,并且AVX包含更多的优秀特性,因此AMD决定支持AVX指令集
Advanced Vector Extensions。较新的Intel CPU都支持AVX指令集, 它可以一次操作256bit数据, 是SSE的2倍,可以使用一条AVX指令一次计算8个float数。AVX指令要求内存地址对齐于32字节边界。


根据参考文章,其中用gcc编译AVX版代码时需要加-mavx选项.
 开启-O3选项,一般不用将代码改成多次计算和内存对齐。
开启-O3选项,一般不用将代码改成多次计算和内存对齐。
gcc -march=native -c -Q --help=target # 查看支持的指令集
g++ -O2 -ftree-vectorize -ftree-vectorizer-verbose=9 -S -c foo.cpp -o /dev/stdout | c++filt # 查看汇编
OBJDUMP # 反汇编
-Rpass=loop-vectorize
identifies loops that were successfully vectorized.
-Rpass-missed=loop-vectorize
identifies loops that failed vectorization and indicates if vectorization was specified.
-Rpass-analysis=loop-vectorize
identifies the statements that caused vectorization to fail.

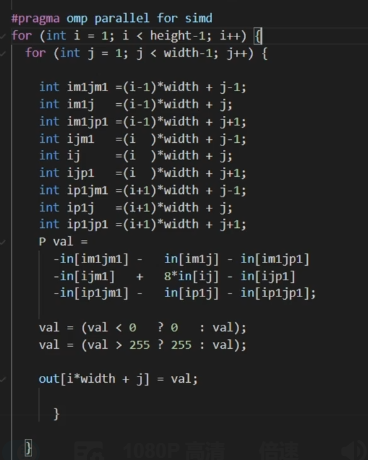 循环展开8次
循环展开8次
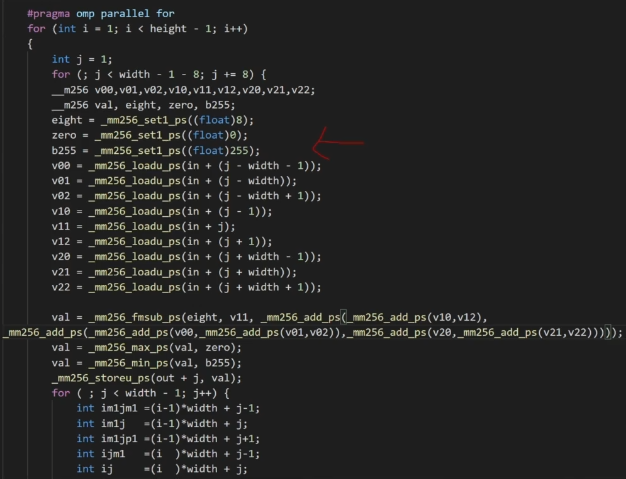
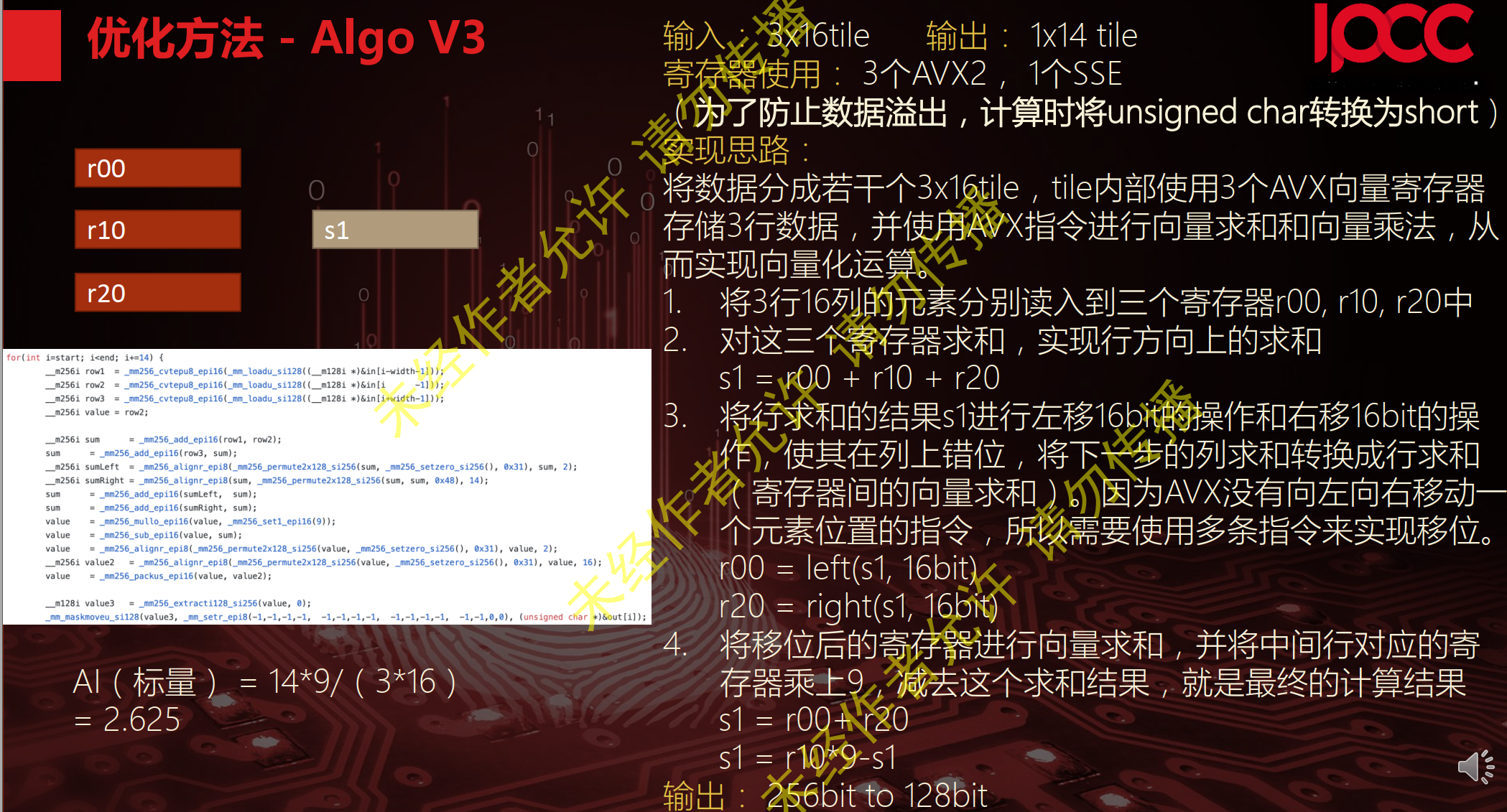
暂无
暂无
https://www.dazhuanlan.com/2020/02/01/5e3475c89d5bd/
https://software.intel.com/sites/landingpage/IntrinsicsGuide/
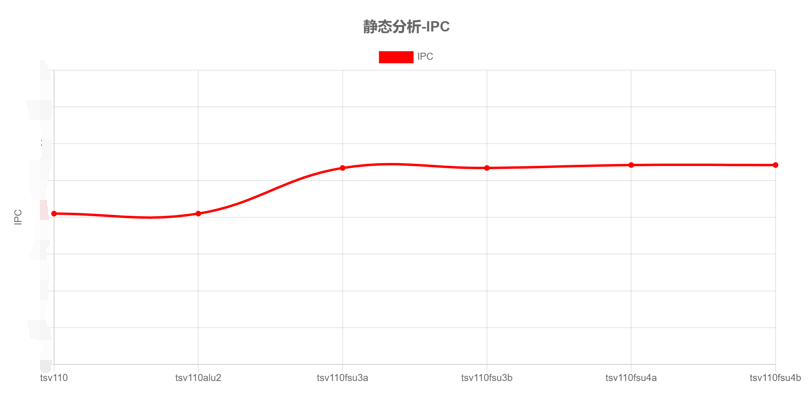
x轴的含义是改变port值的意思,比如tsv110alu2是在tsv110的基础上将alu的值改成2
commit c9ca3a3c66a493d72cf7afc7ee975e2de399f2e5
Author: Elvina Yakubova <[email protected]>
Date: Sat Nov 7 01:50:43 2020 +0300
[AArch64] Add driver tests for HiSilicon's TSV110
commit 93b99728b1676d23ab5dabc606344230d25e7f4b
Author: Elvina Yakubova <[email protected]>
Date: Sat Nov 7 01:22:35 2020 +0300
[AArch64] Add pipeline model for HiSilicon's TSV110
This patch adds the scheduling and cost model for TSV110.
Reviewed by: SjoerdMeijer, bryanpkc
Differential Revision: https://reviews.llvm.org/D89972
commit 123553921f86ac0fad7b742740aa45e8d380be02
Author: Bryan Chan <[email protected]>
Date: Fri Nov 9 19:32:08 2018 +0000
[AArch64] Support HiSilicon's TSV110 processor
Reviewers: t.p.northover, SjoerdMeijer, kristof.beyls
Reviewed By: kristof.beyls
Subscribers: olista01, javed.absar, kristof.beyls, kristina, llvm-commits
Differential Revision: https://reviews.llvm.org/D53908
llvm-svn: 346546
应该每次都要重新编译安装
llvm/test/MC/AArch64下的汇编能用吗?选个最大的,neon 不支持, armv8.2也并不支持。感觉有特别要求
locate at llvm/lib/Target/AArch64/AArch64SchedTSV110.td
tablegen(LLVM class) definitions
InstRW的定义
// Map a set of opcodes to a list of SchedReadWrite types. This allows
// the subtarget to easily override specific operations.
//
// SchedModel ties this opcode mapping to a processor.
class InstRW<list<SchedReadWrite> rw, dag instrlist> {
list<SchedReadWrite> OperandReadWrites = rw;
dag Instrs = instrlist;
SchedMachineModel SchedModel = ?;
// Allow a subtarget to mark some instructions as unsupported.
bit Unsupported = false;
}
def TSV110Wr_2cyc_1MDU : SchedWriteRes<[TSV110UnitMDU]> { let Latency = 2; }
class SchedWriteRes<list<ProcResourceKind> resources> : SchedWrite,
ProcWriteResources<resources>;
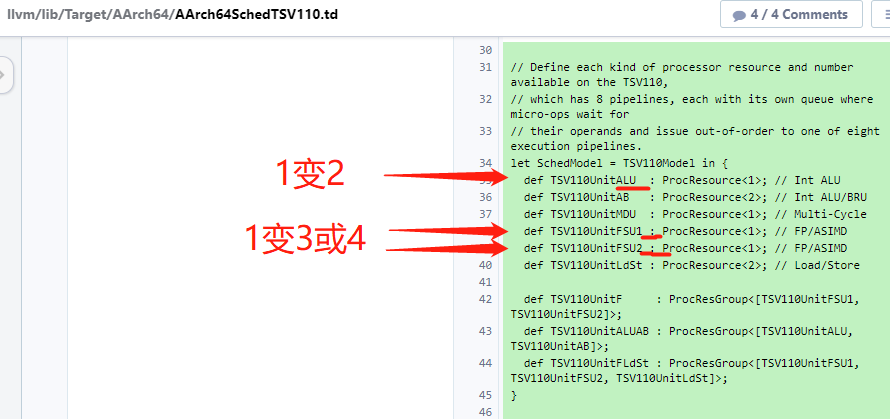
//定义TSV110上可用的每种处理器资源和数量,
//它有8条pipeline管道,每个管道都有自己的队列,微操作在那里等待
//它们的operands和issue将无序地发送到八个执行管道之一。
def TSV110UnitMDU : ProcResource<1>; // Multi-Cycle
暂无
暂无
无
导言
无论是把 PyTorch代码 迁移到其他框架(e.g.,MindSpore),还是把将代码继承到All IN ONE 框架(e.g., MindSpeed-MM),都经常遇到如下头大的问题:
原始的解决办法就是在计算流程上打印关键数据的变化,找到是开始出现了差异(非预期)地方,使用起来非常不方便:
想寻找/开发一个python工具DataDiffer/TensorDiffer:
容易转换成TensorRT
好像是属于NLP问题
https://www.163.com/dy/article/GAPBDHKG0511AQHO.html
https://www.zhihu.com/question/452749603
该篇论文于2003年发表在“Journal of Machine Learning Research”期刊上,迄今引用次数已超过15000次,可见该论文对后来相关研究工作的影响之大。
首次正式将主题以隐变量的形式引入,形成一个三层贝叶斯模型,并且相比于之前和它最接近的pLSI文本模型,LDA的主题选取不再受训练集文本内容的束缚,是一个完全非监督且依据多个主题进行聚类的机器学习、数据挖掘领域的算法。
在推荐系统的研究中,利用评论文本信息来提升推荐性能是近3-4年的一个热门研究领域,LDA及其改良的文本模型则是用来挖掘评论文本的主要方式。
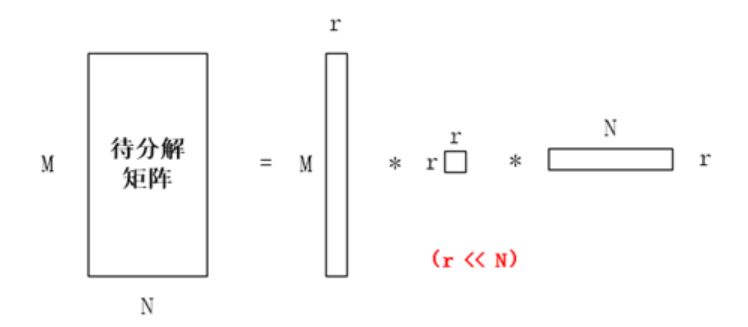
最重要的是LDA模型的两个参数,确定了后能在未知的文本里提取主题
暂无
暂无
https://zhuanlan.zhihu.com/p/28777266
https://blog.csdn.net/fish0058/article/details/25075591
https://blog.csdn.net/anqiu4023/article/details/102275607
https://pypi.python.org/pypi/lda
http://scikit-learn.org/dev/modules/generated/sklearn.decomposition.LatentDirichletAllocation.html#sklearn.decomposition.LatentDirichletAllocation
现代计算机微架构是最复杂的几个人造系统。在上面预测,解释和优化软件是困难的。我们需要其运行行为的可信模型,但是事实是稀缺的。
本文设计和实现了一种构建X86指令的延迟,吞吐量和端口使用的可信模型。并仔细探究了这三个指标的定义。尤其是latency的值在不同的操作数情况时是如何确定的。
同时其结果也是机器可读的。并且对已有的所有Intel架构都进行了测试。
官网有结果 http://www.uops.info
We also plan to release the source code of our tool as open source
balabala~
我们的工具可以用来优化llvm-mca等软件。
Future work includes adapting our algorithms to AMD x86 CPUs. 官网已经实现了。
We would also like to extend our approach tocharacterize other undocumented performance-relevant aspects of the pipeline, e.g., regarding micro and macro-fusion, or whether instructions use the simple decoder, the complex decoder, or the Microcode-ROM.
暂无
暂无
无
一种新的profiler,可以profile没有用户干预的内存访问的基本块。
基于这种profiler创建了BHive,来验证llvm-mca等模型。
BHive是用来评价llvm-mca这些模型的,实验基于各种收集来的一个基本块各种评价
困难在于现有的 没有考虑 memory crash ??? .默认命中L1 cache
A key technical challenge with collecting a large basic block dataset is that there is no existing approach to profile an arbitrary basic block that has been removed from its program context.
(没懂?那为什么要removed from its program context) 因为要把常用的应用拆成小例子来评判,这些模型的准确性。
运用隐含狄利克雷分布LDA,基于cpu资源的利用率,来cluster benchmark suite里的基本块
通过对各种类型最基本的代码块来进行profile,从而形成针对各种performance model的数据库。
现在已经有超过30万的基本块分析,来源于各种方向的应用,包括数值计算OpenBLAS,数据库SQLite,机器学习TensorFlow,密码学OpenSSL。
这么多的数据产生了一个用于评估performance model的新benchmark。
作者说performance modeling 研究的未来在于与其他先进技术的大规模定量比较
通过把虚拟页面映射到单个物理页面,来合法内存访问同时避免cache miss
有两种model 1. 产生可以详细描述指令何时发射和退休的可解释执行路径的微架构模拟器,附带吞吐量预测。 2. 每条指令都有延迟、吞吐量查找表,相当于一个被寄存器分配器使用的额外开销估计器
各种model, 写到另一篇里了
unroll factor(典型值是100)unroll factor就是循环展开次数。目标是在不需要手动干预的情况下分析任意基本块,以便测量的吞吐量与性能模型通常假定的定义和不变量相对应。关键的挑战是使这些基本块能够在不崩溃的情况下访问任意内存地址。
由于基本块只是正常程序的一部分,导致根本不能单独正常运行。BHive做的事情就是,让他正常运行。
 这个代码块只有执行代码分配在
这个代码块只有执行代码分配在0x4110a时,才能正常运行
1. Remapping Virtual Pages.
1. 一个基本块的所有虚拟内存页重新映射到一个物理页上,所以全部数据访问都命中L1。这样就可以执行97%的基本块。
2. 步骤
1. 把原本虚拟页全部unmap
1. 这会导致除了包含基本块指令的页之外的全部的连续的内存访问出问题???
2. 在子进程里运行展开的基本块指令。
1. 这时对每个unmap的虚拟页的访问都会出错,但是主进程一种监视着。一旦中断就重新映射出错地址,然后重新开始跑。
2. Memory Initialization
1. 初始化一个中等大小0x12345600的物理页,允许都虚拟页都映射
3. Virtual page aliasing
1. 因为不同的虚拟页映射在同一个物理页的同一项导致memory dependences,要等待
2. 剔除6.28%的基本块
3. 可以通过增大物理页,来减小发生的概率。
通过重复运行基本块来计算吞吐量
1. Raw Measurement
1. 先从基本块里,产生不会memory crash的可执行部分。
2. unroll factor的选取。It uses 100 and 200 as the unroll factors for basic blocks smaller than 100 bytes; 50 and 100 for basic blocks between 100 bytes and 200 bytes; and finally 16 and 32 for basic blocks larger than 200 bytes
2. Filtering
1. 筛选执行代码满足理想化模型的执行结果,比如命中L1cache
2. L1 Cache Misses
1. 工具可以用硬件计数器监控指令和数据cache misses。拒绝所有cache miss的情况。
3. Unaligned Loads
1. 不连续的访存会很慢,解决方法就是去除所有有不连续的访存的。大约删除了0.18%的基本块
4. Subnormal Floating Point
1. 一些特殊的浮点数计算会比正常的浮点数计算慢20倍,去除了与MXCSR寄存器有关的0.1%的基本块。
2. https://stackoverflow.com/questions/8341395/what-is-a-subnormal-floating-point-number
5. Context Switches
1. 上下文切换(英语:context switch),又称环境切换,电脑术语,是一个存储和重建CPU的状态 (内文),因此令多个进程(process)可以分享单一CPU资源的计算过程。要切换CPU上的进程时,必需先行存储目前进程的状态,再将欲运行的进程之状态读回CPU中。
6. 可接受的评估公式 10%的误差???
3. Throughput Calculation
1. 如果通过了基本块的筛选,用有记录的最小延迟计算吞吐量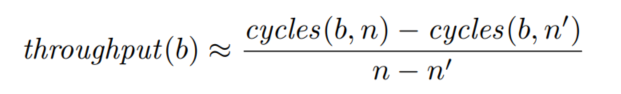 4. Environment Variance
1. 由于环境的影响,导致结果有个稳定的偏移。至少执行5次,展开16次的基本块。取最小的5次作为结果。
4. Environment Variance
1. 由于环境的影响,导致结果有个稳定的偏移。至少执行5次,展开16次的基本块。取最小的5次作为结果。
只要架构满足以下几点要求 1. 有将多个虚拟页面映射到几个物理页面的API。map multiple virtual pages to a few physical pages 1. without incurring a performance penalty due to unnecessary cache invalidation. We therefore require that the target processor has a physically tagged data cache(VIPT)??? 1. we additionally require that the page size is small enough so the indexing bits are not affected by address translation. 1. detecting cache misses, 2. and detecting or disabling floating-point underflow.
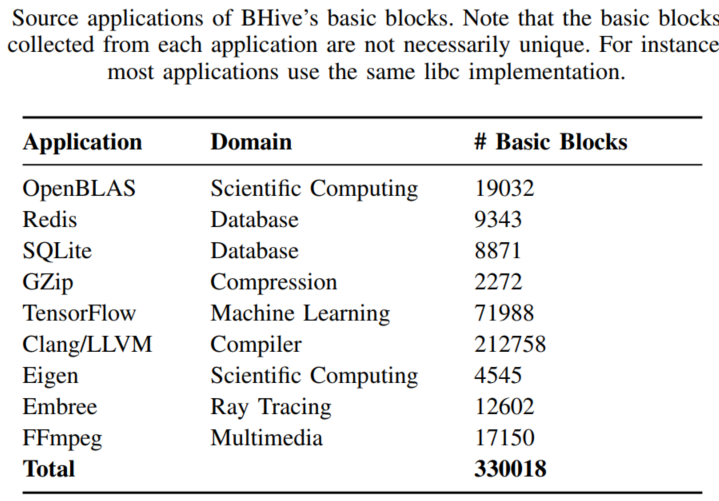
应用的选择
We compiled all applications with the highest optimization settings defined by their build systems. 如果可以用上了AVX2。
使用DynamoRIO动态分析来提炼基本块。可以实现在运行时记录每个运行的基本块。我们采用动态分析,而不是静态反汇编。因为静态反汇编无法区别padding bytes from instructions。???
应用的例子除了FFmpeg and Gzip都是选择的官方的benchmark。 Eigen 采用的是 two sparse linear algebra workloads: sparse matrix-matrix multiplication (SpMM) and sparse matrix-vector multiplication (SpMV).
一些基本块比其他的更难建模,???(建什么模,VI-B说明了什么)有内存依赖的基本块预测错误率更高。
采用了一种技术???(是应用在提取上) 基于处理器的使用聚类基本块。 这个技术有助于性能模型的设计和使用者更细粒度了解performance model,让他们能集中以后新添加的资源在有困难的那一类基本块。
xor %rax, %rbx in Haswell is {p0156 → 1}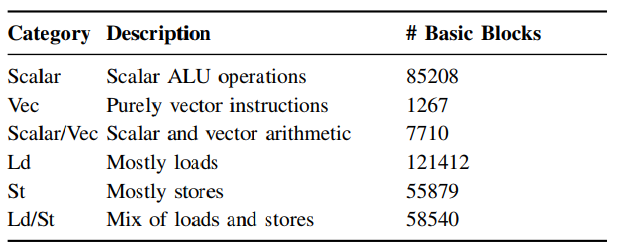


在3种Intel架构上验证4种已有的性能模型
1. Methodology
1. 说明各个测试软件的版本。
2. Dataset
1. basic block dataset discussed in Section IV
3. Platform
1. balabala 3种架构的 Intel cpus
4. Evaluation Metrics
1. 测量吞吐量t和预测吞吐量t'$\(err(t,t')=|\frac{t-t'}{t}|\)$
2. 不以预测精度,而是以预测结果的相对关系为评分标准。
5. 额外能评估每个模型如何保持基本块吞吐量的顺序。使用Kendall’s tau系数(越大效果越好),而不是相对误差。测量的原因是使用者可能关心的不是绝对的数值精度,而是相对关系的准确率。比如优化软件的时候关心的不是具体耗时,而是哪个优化策略耗时更短。
2. Results
1. 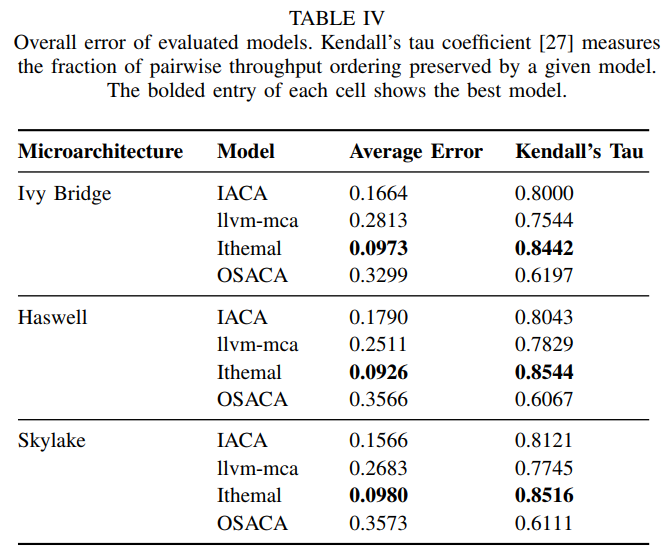 2. IACA 第二好的,在向量化类模拟的最好
3. llvm-mca 最差的,尤其是和loads有关时。
4. Ithemal 除了向量基本块都是最好的。在memory dependence (Ld/St)尤其好,但是向量基本块不好,可能与训练集没有向量基本块有关。
5. OSACA 第三。由于还在开发中,使用还遇到5个bug。在遇到一些不认识的指令的时候,会直接按照nops空指令处理。
3. Examples of Modeling Bugs
2. IACA 第二好的,在向量化类模拟的最好
3. llvm-mca 最差的,尤其是和loads有关时。
4. Ithemal 除了向量基本块都是最好的。在memory dependence (Ld/St)尤其好,但是向量基本块不好,可能与训练集没有向量基本块有关。
5. OSACA 第三。由于还在开发中,使用还遇到5个bug。在遇到一些不认识的指令的时候,会直接按照nops空指令处理。
3. Examples of Modeling Bugs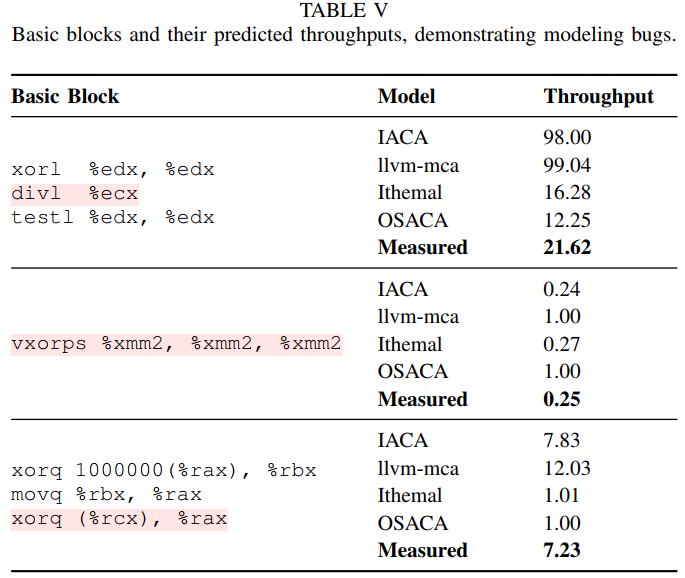 1. 最后一个例子是由于模型错误调度微指令导致的
2. Modeling bug due to unsigned division
1. 例子是 a 64-bit by 32-bit unsigned division.
1. 最后一个例子是由于模型错误调度微指令导致的
2. Modeling bug due to unsigned division
1. 例子是 a 64-bit by 32-bit unsigned division.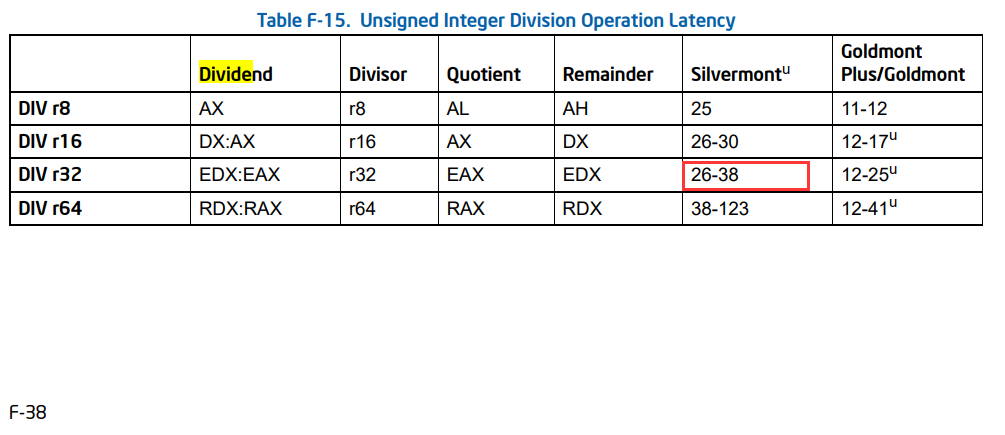
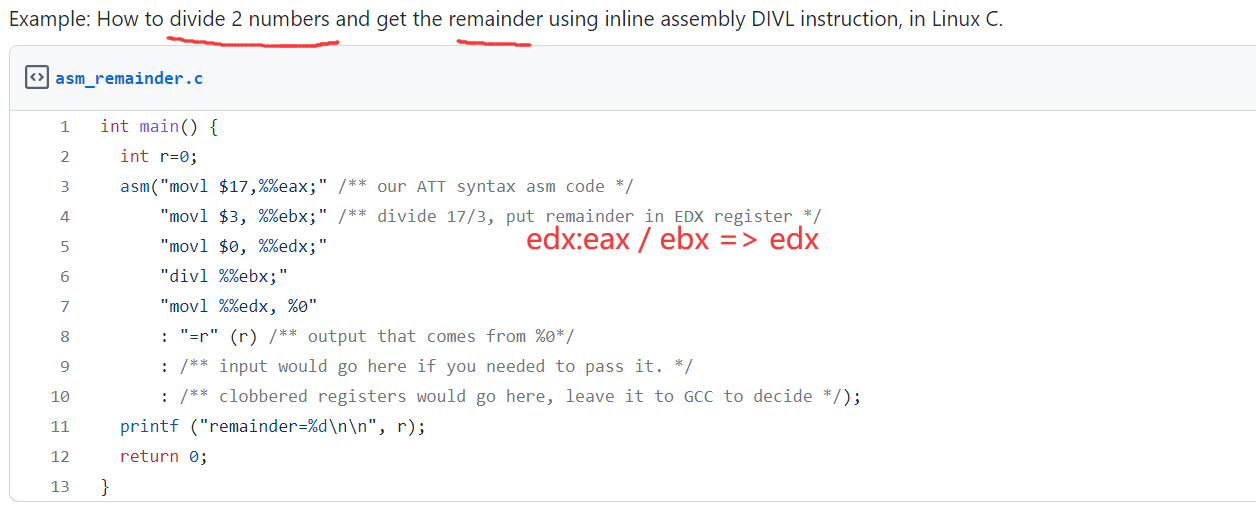

 2. ???
2. ??? 3. Modeling bug due to zero-idioms
1.
3. Modeling bug due to zero-idioms
1.  2. 对这种结果固定的特殊指令的快速处理。
4. Modeling bug due to mis-scheduling
1. 对于数据依赖,上下指令的寄存器有写后读。
2. Ithemal’s and OSACA忽略了该依赖
3.
2. 对这种结果固定的特殊指令的快速处理。
4. Modeling bug due to mis-scheduling
1. 对于数据依赖,上下指令的寄存器有写后读。
2. Ithemal’s and OSACA忽略了该依赖
3.  4. llvm-mca 没有注意到(%rcx)是memory,没有依赖可以提前发射。
4. llvm-mca 没有注意到(%rcx)是memory,没有依赖可以提前发射。
现有的静态分析器对内存依赖和向量化块的建模还有困难。
benchmark/sources下是各种软件的各个部分的16进制基本代码块和其出现概率,用csv格式(逗号分隔值 (Comma-separated values))存储benchmark/throughput是在各种架构下的各基本块的测量吞吐量,单位cycles per hundred-iterations.
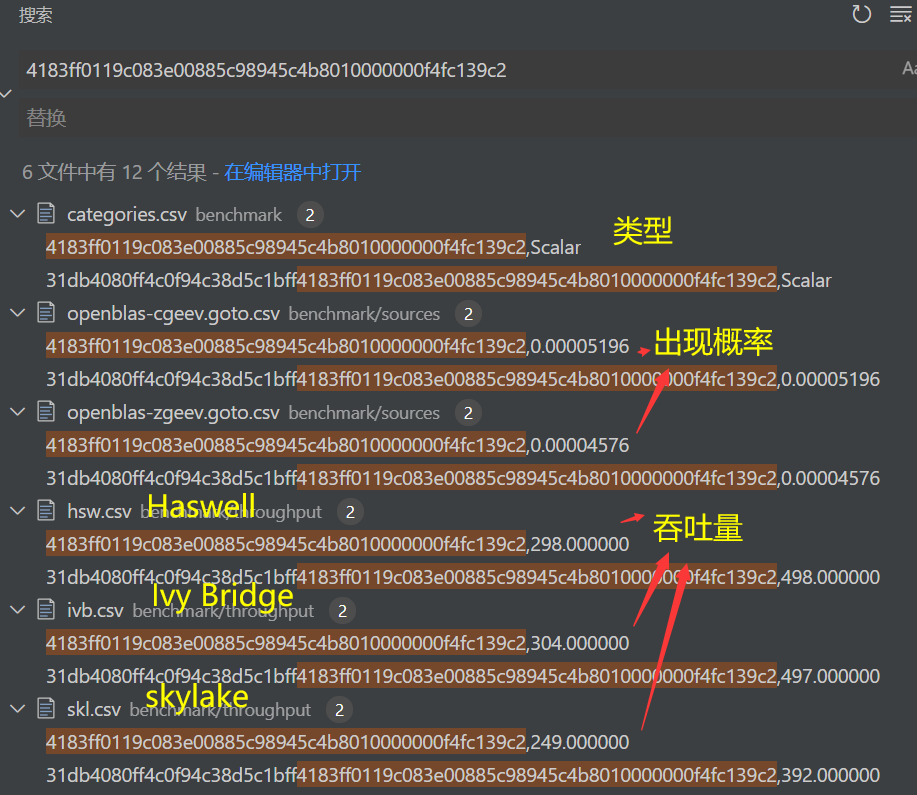
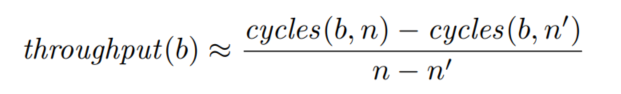
benchmark/disasm可以把16进制代码通过nasm变成汇编,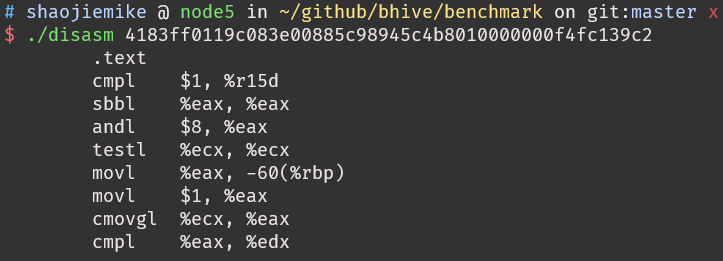
timing-harness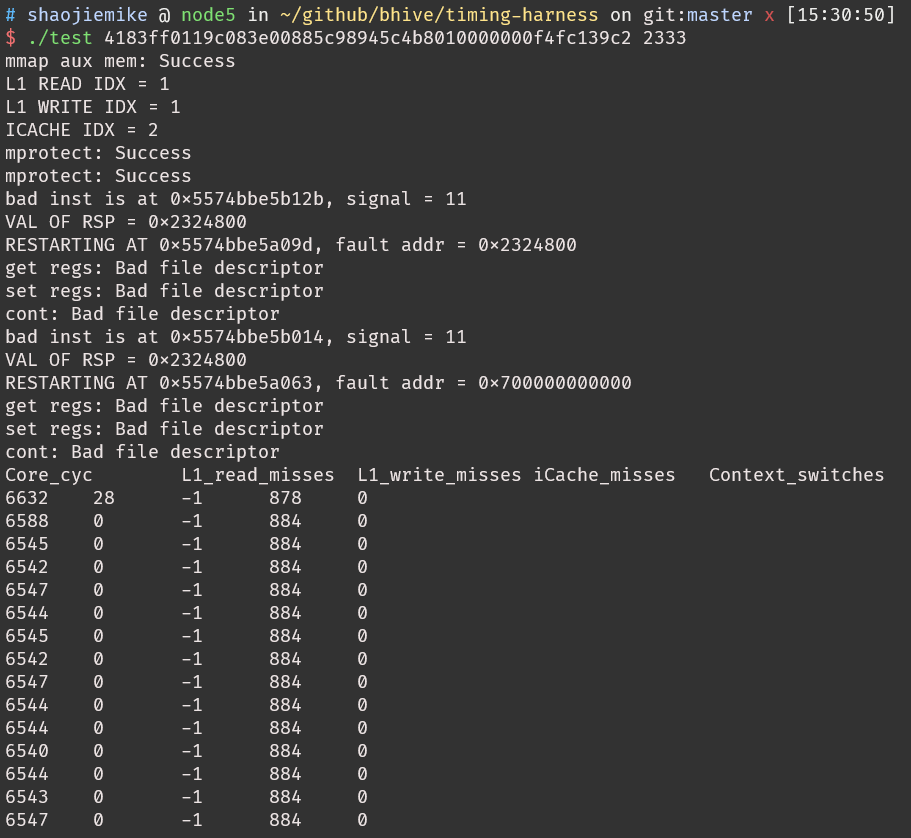
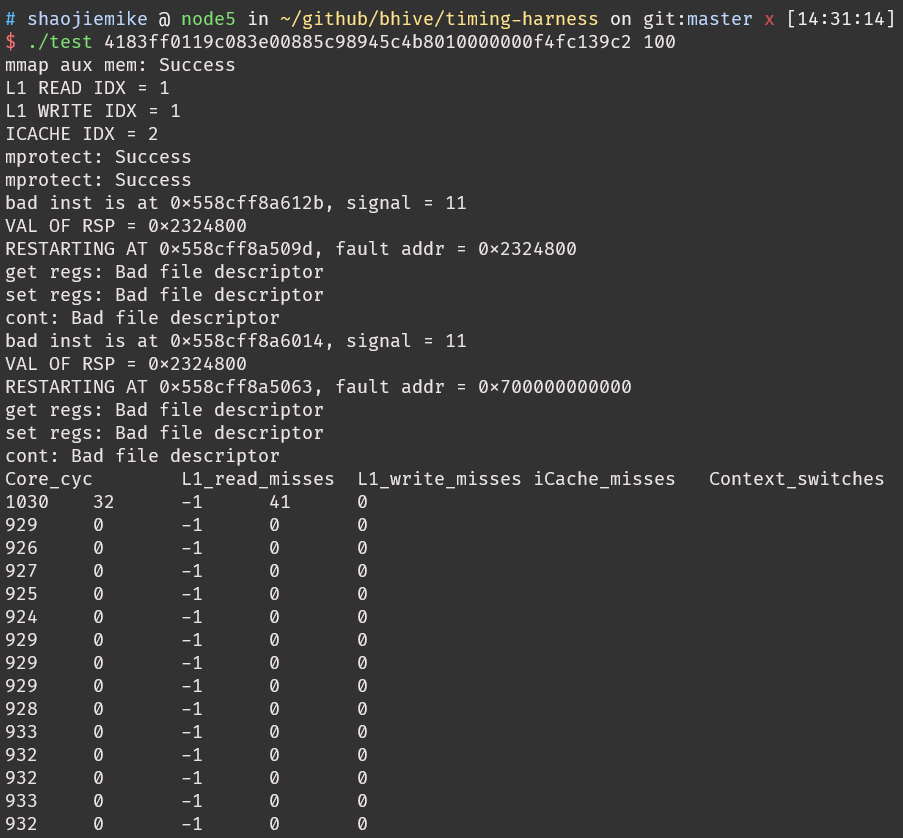 吞吐量的计算(猜的)Skylake microarchitecture$\(\frac{6632-1030}{2333-100}*100=250.8 (cyc/hundred\ iters)\)$
吞吐量的计算(猜的)Skylake microarchitecture$\(\frac{6632-1030}{2333-100}*100=250.8 (cyc/hundred\ iters)\)$uops 的文章, Accurate Throughput Prediction of Basic Blocks on Recent Intel Microarchitectures
4.2 Extending BHive
hhex2bin转换为二进制create_shm_fd

shm_open, shm_unlinkcreates and opens a new, or opens or unlink an existing, POSIX shared memory object. O_RDWR Open the object for read-write access.O_CREAT the shared memory object if it does not exist. 777是类似文件读写执行组权限的东西 On success, shm_open() returns a file descriptor (a nonnegative integer)
POSIX可移植操作系统接口The Portable Operating System Interface 是IEEE为要在各种UNIX操作系统上运行软件,而定义API的一系列互相关联的标准的总称。
ftruncate — truncate截短 a file to a specified lengthmeasure开始测量pipe用于创建pipe,用来进程间通信的单向数据通路,传入变量用来返回引用自pipe末端的文件描述符file descriptors。第一个指向the read end of the pipe,第二个指向the write end of the pipemmap(void *addr, size_t length, int prot, int flags,int fd, off_t offset); munmap(void *addr, size_t length);- map or unmap files or devices into memory 在调用进程的虚拟地址空间里create a new mapping.attach_to_child(pid, fds[1]); pid是子进程pidptrace(enum __ptrace_request request, pid_t pid,void *addr, void *data) - process trace 提供一种进程tracer跟踪控制另一个进程tracee的方法,可以修改被控制者的memory and registers.PTRACE_SEIZE Attach to the process specified in pid, making it a tracee of the calling process. Unlike PTRACE_ATTACH, PTRACE_SEIZE does not stop the processrdpmc_open_attr initialize a raw ring 3 ReaDable PerforMance Counterwait挂起当前线程,直到有一个children结束,返回其PIDWIFEXITEDWait_IF_EXITED 判断是否正常结束
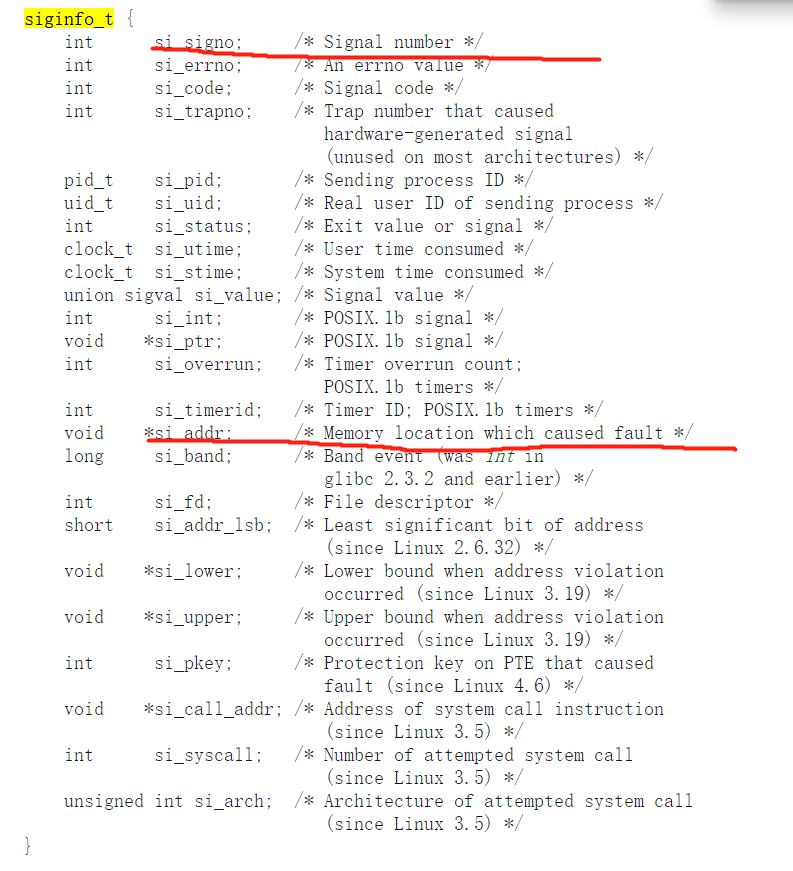
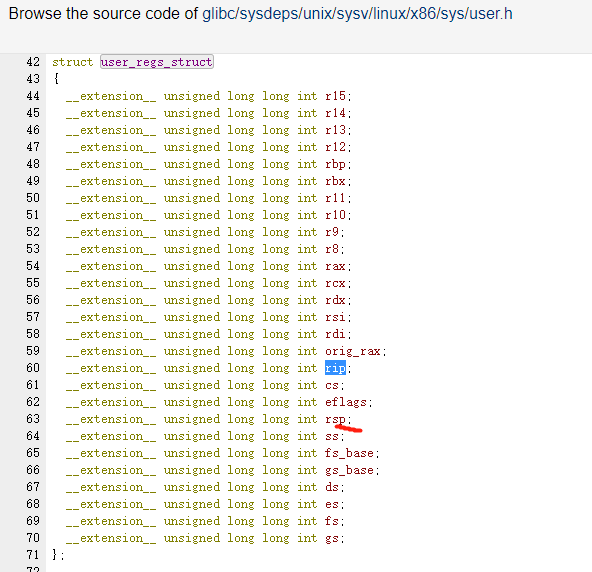
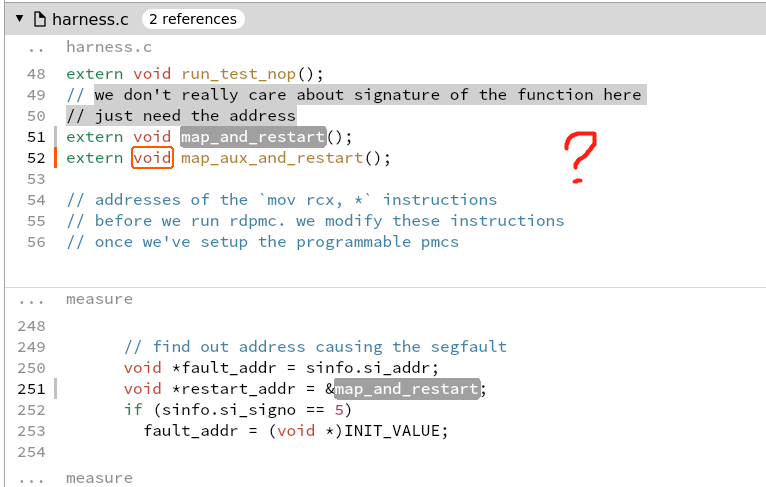

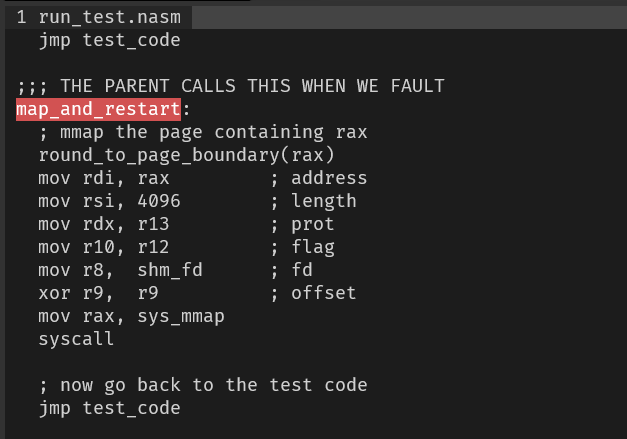
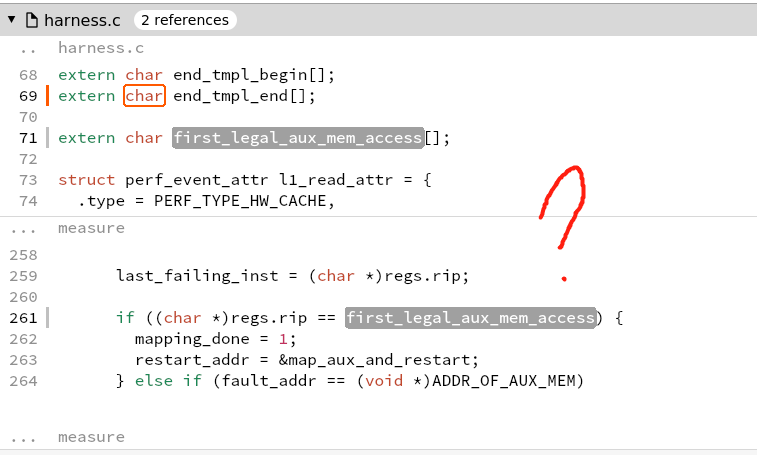
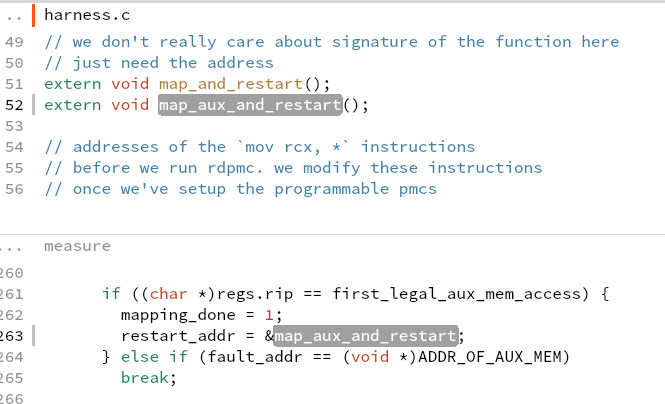 what is aux mem?
what is aux mem?PTRACE_CONT Restart the stopped tracee process
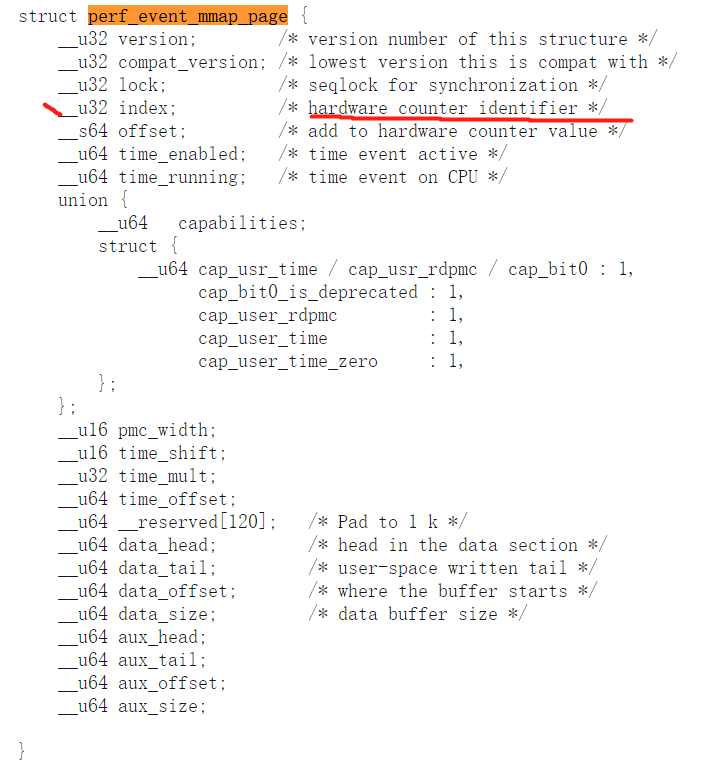
https://www.cnblogs.com/from-zero/p/13750852.html
暂无
问题是x86的二进制或者汇编不能变成aarm64的二进制或者汇编。
https://github.com/ithemal/bhive