Algorithms¶

2023年11月15日
分类于 Algorithms
需要 1 分钟阅读时间

Data Structure Summary

导言

ASCYLIB (with OPTIK) is a concurrent data-structure library. It contains over 40 implementations of linked lists, hash tables, skip lists, binary search trees (BSTs), queues, priority queues, and stacks. ASCYLIB contains sequential, lock-based, and lock-free implementations for each data structure.

2023年10月16日
分类于 Algorithms
需要 1 分钟阅读时间

Concurrent-AMAT, C-AMAT

并发式平均存储访问时间模型

APC

侧重于测量方法的研究，给出了并发存储的测量方法和尺度。

在 APC 中，周期是存储活动周期 (memory active cycle)，不是通用的 CPU 周期，所以 APC 也叫 APMAC（存储活动周期平均访问数， access per memory active cycle）。

同时 APC 采用重叠 (overlapping) 的访存时间统计方法：在有两个或多个存储访问同时进行时，周期只增加一次。

2023年10月16日
分类于 Algorithms
需要 2 分钟阅读时间

HPL.dat file detailed explanation

HPL.dat

HPLinpack benchmark input file
Innovative Computing Laboratory, University of Tennessee
HPL.out      output file name (if any) 输出文件名
6            device out (6=stdout,7=stderr,file)

1            # of problems sizes (N) = sqrt((Memory Size in Gbytes * 1024 * 1024 * 1024) /8) * ratio
11136         Ns 矩阵规模

1            # of NBs block sizes (64~512)In the [96,104,112,120,128, …, 256] range; the multiple of 64
96           NBs 矩阵分块方法

0            PMAP process mapping (0=Row-,1=Column-major) 选择处理器阵列是按列的排列方式还是按行的排列方式。

1            # of process grids (P x Q)
2            Ps # two-dimensional block-cyclic data distribution = amount of processes; P≤Q
2            Qs 二维处理器网格（P×Q）

16.0         threshold 阈值

1            # of panel fact # 后面是L分解的方式
2            PFACTs (0=left, 1=Crout, 2=Right)
1            # of recursive stopping criterium
4            NBMINs (>= 1)
1            # of panels in recursion
2            NDIVs
1            # of recursive panel fact.
1            RFACTs (0=left, 1=Crout, 2=Right)
1            # of broadcast
1            BCASTs (0=1rg,1=1rM,2=2rg,3=2rM,4=Lng,5=LnM)
1            # of lookahead depth
1            DEPTHs (>=0)
2            SWAP (0=bin-exch,1=long,2=mix)
64           swapping threshold
0            L1 in (0=transposed,1=no-transposed) form
0            U  in (0=transposed,1=no-transposed) form
1            Equilibration (0=no,1=yes)
8            memory alignment in double (> 0)

合适的参数参考

2023年9月25日
分类于 Algorithms
需要 14 分钟阅读时间

Leetcode

导言

简单、中等、困难在10、20、30分钟解决（倒计时计数
题解在5、10、20分钟内理解，明白核心考点和解题思想，然后重写。
ACM模式练习

做了30天的leetcode，发现不会的还是不会。我就知道我

学而不思则罔

脑中一团浆糊，虽然学习了一些常见题型的框架、解法以及例题。

但是遇到新题目，是否能使用这些方法，以及如何转换使用还是没考虑清楚。

2023年8月28日
分类于 Algorithms
需要 1 分钟阅读时间

Graph Algorithms: Pagerank

Pagerank

Network and social network can be identified as a weighted graph
How to do the important ranking is Pagerank

how to design a graph when pr executing memory access jump data-array very random?

需要进一步的研究学习

暂无

遇到的问题

暂无

开题缘由、总结、反思、吐槽~~

参考文献

上面回答部分来自ChatGPT-3.5，没有进行正确性的交叉校验。

https://zhuanlan.zhihu.com/p/137561088

2023年8月3日
分类于 Algorithms
需要 2 分钟阅读时间

Benchmark : GUPS

Introduction

GUPS (Giga十亿 UPdates per Second) is a measurement that profiles the memory architecture of a system and is a measure of performance similar to MFLOPS.

The HPCS HPCchallenge RandomAccess benchmark is intended to exercise the GUPS capability of a system, much like the LINPACK benchmark is intended to exercise the MFLOPS capability of a computer. In each case, we would expect these benchmarks to achieve close to the "peak" capability of the memory system. The extent of the similarities between RandomAccess and LINPACK are limited to both benchmarks attempting to calculate a peak system capability.

definition of GUPS

GUPS is calculated by identifying the number of memory locations that can be randomly updated in one second, divided by 1 billion (1e9).

The term "randomly" means that there is little relationship between one address to be updated and the next, except that they occur in the space of one half the total system memory. （只用一半内存？）
An update is a read-modify-write operation on a table of 64-bit words. An address is generated, the value at that address read from memory, modified by an integer operation (add, and, or, xor) with a literal value, and that new value is written back to memory.

Extensibility

We are interested in knowing the GUPS performance of both entire systems and system subcomponents --- e.g., the GUPS rating of a distributed memory multiprocessor the GUPS rating of an SMP node, and the GUPS rating of a single processor.
While there is typically a scaling of FLOPS with processor count, a similar phenomenon may not always occur for GUPS.

Principle

Select the memory size to be the power of two such that 2^n <= 1/2 of the total memory. Each CPU operates on its own address stream, and the single table may be distributed among nodes. The distribution of memory to nodes is left to the implementer. A uniform data distribution may help balance the workload, while non-uniform data distributions may simplify the calculations that identify processor location by eliminating the requirement for integer divides. A small (less than 1%) percentage of missed updates are permitted.

Installation

Download

official web or from GitHub

Usage

需要进一步的研究学习

暂无

遇到的问题

暂无

开题缘由、总结、反思、吐槽~~

参考文献

上面回答部分来自ChatGPT-3.5，没有进行正确性的交叉校验。

无

2023年7月24日
分类于 Algorithms
需要 3 分钟阅读时间

Dynamic Programming

动态规划简介

将一件事情分成若干阶段，然后通过阶段之间的转移达到目标。由于转移的方向通常是多个，因此这个时候就需要决策选择具体哪一个转移方向。

动态规划所要解决的事情通常是完成一个具体的目标，而这个目标往往是最优解。并且：

阶段之间可以进行转移，这叫做动态。
达到一个可行解(目标阶段) 需要不断地转移，那如何转移才能达到最优解？这叫规划。

每个阶段抽象为状态（用圆圈来表示），状态之间可能会发生转化（用箭头表示）。可以画出类似如下的图：

性质：

最优子结构
问题的最优解所包含的子问题的解也是最优的
注意：具有最优子结构也可能是适合用贪心的方法求解。
无后效性
已经求解的子问题，不会再受到后续(父问题)决策的影响。
即子问题的解一旦确定，就不再改变，不受在这之后、包含它的问题的求解决策的影响。
子问题重叠
如果有大量的重叠子问题，我们可以用空间将这些子问题的解存储下来，避免重复求解相同的子问题，从而提升效率。

基本思路

对于一个能用动态规划解决的问题，一般采用如下思路解决：

将原问题划分为若干阶段，每个阶段对应若干个子问题，提取这些子问题的特征（称之为状态）；
寻找每一个状态的可能决策，或者说是各状态间的相互转移方式（用数学的语言描述就是状态转移方程）。
按顺序求解每一个阶段的问题。如果用图论的思想理解，我们建立一个有向无环图，每个状态对应图上一个节点，决策对应节点间的连边。

难点，重点

如何找到转移关系：

可以伸缩的维度：一般是数组的下标，或者是字符串的下标，或者是树的节点。也可以是问题的query数值。
分情况讨论的，最大值为不同情况的最大值。方案数为所有情况的总和。

DP分类

背包DP
0-1背包
- 定义：每个物体只有两种可能的状态（取与不取），对应二进制中的 0 和 1，这类问题便被称为「0-1 背包问题」
- 一般有个总cost为W来限制选择
- 基础版：可以通过滚动数组减少空间占用，但是注意遍历方向
- 常见变形：
- 至多装capacity,求方案数/最大价值和
- 恰好装capacity,求方案数/最大/最小价值和
  - 方案数，将转移公式最大值，改成加法。注意会多一维度数据。基础1+提升2
- 至少装capacity,求方案数/最小价值和
- 变种：总cost等于W时，和为half的子集是否存在
- 方法一：
  - 背包的体积为sum / 2
  - 每个物品 cost = value
  - 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
- 方法二：
  - 状态：前i个元素，和为j的子集是否存在
  - 转移关系: \( f(i,j)=(f(i-1,j)+f(i-1,j-a[i])>0)?1:0 \) 注意： f[i,0]=1
- 变种：选择和为k的子集的
- 变种2：总cost等于W时，和为half的子集的个数题目：2022.9.23-求和
- 状态：前i个元素，和为j的子集个数
- 转移关系: \( f(i,j)=f(i-1,j)+f(i-1,j-a[i]) \) 注意： f[i,0]=1
完全背包: 每个物体可以选择多次
- 转移关系: 也可以由f(i, j-w)转移到f(i,j)
多重背包: 每个物体可以选择\( k_i \)次
- 朴素思路: 每步可以总\( k_i \)里选最大, \( f_{i,j} = max_{k=0}^{k_i}(f_{i-1,j - k \times w_{i}} + v_{i} \times k ) \)
- 二进制分组优化
- 思想：多重背包，其实是有很多重复元素的0-1背包，通过二进制来唯一表示选取，来最小0-1背包的可选物品数
- 具体操作: 方法是：将第 i 种物品分成若干件物品，其中每件物品有一个系数，这件物品的费用和价值均是原来的费用和价值乘以这个系数。使这些系数分别为\( 1,2,4,\ldots,2^{k-1},n-2k+1 \)，且 k 是满足\( n[i]-2^k+1>0 \)的最大整数。例如，如果 n[i] 为 13，就将这种物品分成系数分别为 1, 2, 4, 6 的 4 件物品。
- 效果：将第 i 种物品分成了 O(log⁡n[i]) 种物品，将原问题\( O(V\times\sum n[i]) \)转化为了复杂度为\( O(V\times\sum \log n[i]) \)的 01 背包问题
```
int num[maxn][2], dp[maxn];
int N, V, c, w, n, tot;
memset(dp, 0, sizeof dp);
cin >> V >> N; tot = 1;
for(int i = 1; i <= N; ++i)
{
  cin >> c >> w >> n; // 第 i 物品的费用、价值和数量
  for(int k = 1; k < n; k<<=1)//左移求下一个所需二进制数 
  {
    num[tot][0] = k*c; // 添加 子物品
    num[tot++][1] = k*w;
    n -= k;
  }
  num[tot][0] = n*c; // 添加n[i]-2^k+1的 子物品
  num[tot++][1] = n*w;
}
for(int i = 1; i < tot; ++i)
{
  for(int j = V; j >= num[i][0]; --j) // 0-1 背包 滚动数组实现
    dp[j] = max(dp[j], dp[j-num[i][0]]+num[i][1]);
}
```
- 单调队列优化 to finish
区间DP
\( f(i,j)=max_k{f(i,k)+f(k+1,j)+cost} \)
DAG 上的DP
DAG(Directed Acyclic Graph) 即有向无环图，一些实际问题中的二元关系都可使用 DAG 来建模，从而将这些问题转化为 DAG 上的最长（短）路问题。
to do
树形 DP 往往需要递归DFS
分阶段参数：当前子树的根节点
转移关系：当前子树的根节点和其子节点的关系
例题： to do

记忆化搜索

子问题间重叠的部分会有很多，同一个子问题可能会被重复访问多次，效率还是不高。
思路: 记忆化，参数一定，那么返回值也一定不会变，因此下次如果碰到相同的参数，我们就可以将上次计算过的值直接返回，而不必重新计算。这样节省的时间就等价于去除的重叠子问题的耗时。
解决方法：把每个子问题的解存储下来，通过记忆化的方式，确保每个子问题只被计算一次。

如何写记忆化搜索

方法一
把这道题的 dp 状态和方程写出来
根据它们写出 dfs 函数
添加记忆化数组
方法二
写出这道题的暴搜程序（最好是 dfs)
将这个 dfs 改成「无需外部变量」的 dfs
添加记忆化数组

实例：朴素DFS递归，实现记忆化

爬楼梯问题的暴力普通递归DFS代码

function climbStairs(n) {
  if (n === 1) return 1;
  if (n === 2) return 2;
  return climbStairs(n - 1) + climbStairs(n - 2);
}

添加与DFS参数相关的记忆化数组，将这个 dfs 改成「无需外部变量」的 dfs。

memo = {}
def climbStairs(n):
  if n == 1:return 1
  if n == 2: return 2
  if n in memo: return memo[n]
  ans = func(n - 1) + func(n-2)
  memo[n] = ans
  return ans
climbStairs(10)

优化技巧

状态压缩 & 动态规划

状压+动态规划(DP, Dynamic Programming)

使用的数有限（共 10 个），并且使用到的数最多出现一次，容易想到使用「状压 DP」来求解：我们使用一个二进制数来表示具体的子集具体方案。

定义 f[state] 为当前子集选择数的状态为 state 时的方案数，state 为一个长度 10 的二进制数，若 state 中的第 k 位二进制表示为 1，代表数值 p[k] 在好子集中出现过；若第 k 位二进制表示为 0 代表 p[k] 在好子集中没出现过。

状态压缩

状态压缩有关，比如用 4 个字节存储状态

需要进一步的研究学习

动态规划与 np完全的关系

遇到的问题

暂无

开题缘由、总结、反思、吐槽~~

参考文献

视频： https://www.bilibili.com/video/BV1Xj411K7oF/?vd_source=5bbdecb1838c6f684e0b823d0d4f6db3

https://oi-wiki.org/dp/basic/

https://www.zhihu.com/question/316416327/answer/626807333

2023年6月4日
分类于 Algorithms
需要 4 分钟阅读时间

Algorithm: leetcode

导言

计算机笔试，以及华为可信科目一相关的常见算法。

2022年9月14日
分类于 Algorithms
需要 3 分钟阅读时间

Hash map

导言

IPCC比赛的时候，发现用hash map会比红黑树的map慢。感觉不对劲，我hash空间声明大，冲突不就低了吗？

2021年8月9日
分类于 Algorithms
需要 3 分钟阅读时间

Parallel BFS

常规广度优先搜索的局限性

简单bfs是每次从队列中取出当前的访问节点后，之后就将它的邻接节点加入到队列中，这样明显不利于并行化。

实现一：两队列

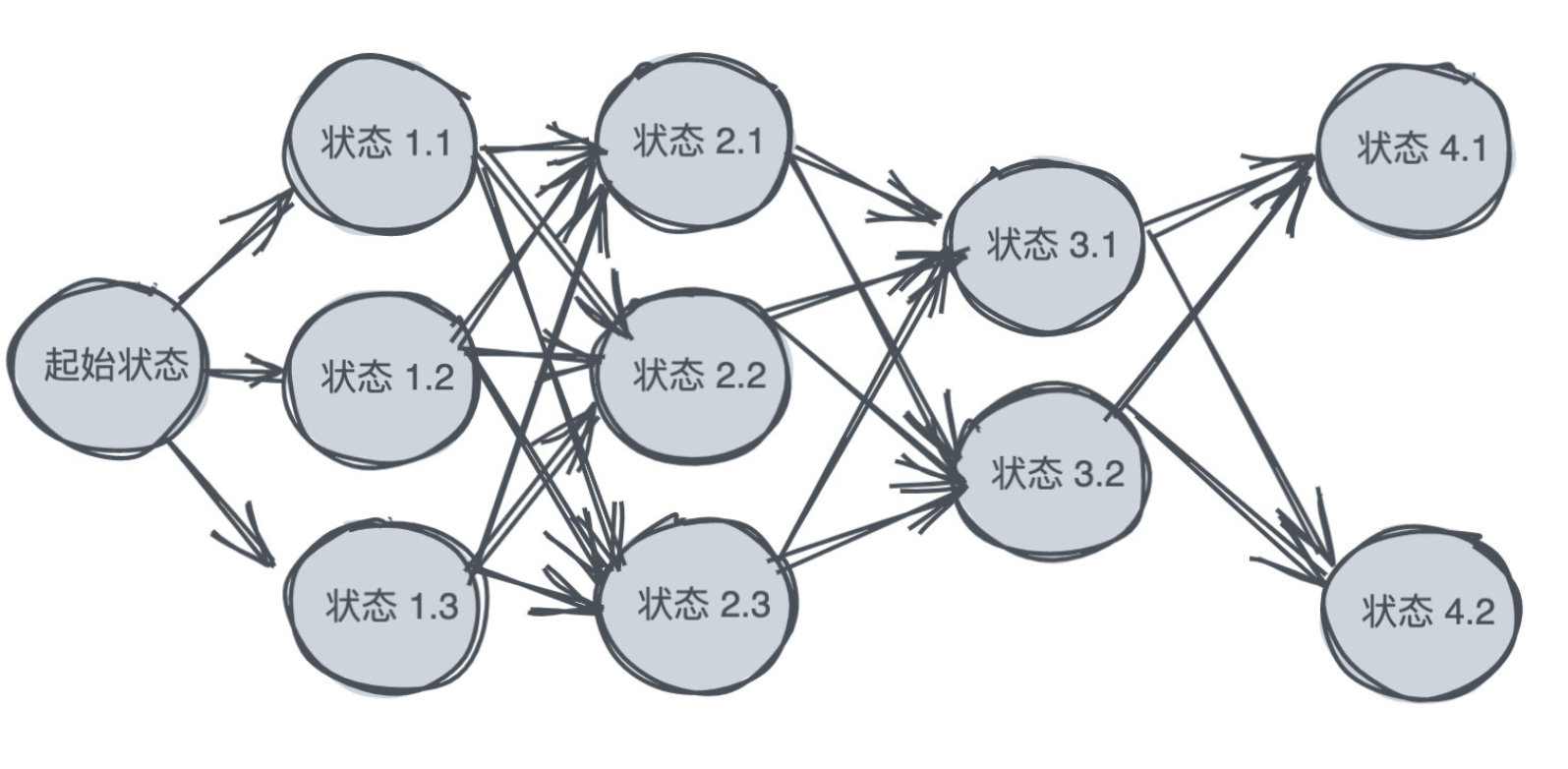
使用了两个队列，第一个队列存当前同一层的节点，第二个队列用来存储当前层节点的所有邻接节点(下一层节点)，等到当前层的节点全部访问完毕后，再将第一个队列与第二个队列进行交换，即可。

这样做的优势在于便于以后的并行化。同一层的节点可以一起运行，不会受到下一层节点的干扰。

但是写有问题，并行计算要储存下一层节点时，push操作不是原子的，需要加锁。

name="__codelineno-0-1" href="#__codelineno-0-1">q1.push(1); distance[1]=0; while(!q1.empty()){ clear(q2); for(int i=0;i<q1.size();i++){ int node=q1.front(); q1.pop(); cout<<node<<"->"; int start_edge=g.outgoing_starts[node]; int end_edge=(node==g.num_nodes-1)?g.num_edges:g.outgoing_starts[node+1]; for(int j=start_edge;j<end_edge;j++){ int outgoing=g.outgoing_edges[j]; if(distance[outgoing]==-1){ distance[outgoing]=1; q2.push(outgoing); } } } swap(q1, q2); }

实现二：PBFS

思想和实现一一样，但是对并行时竞争情况有处理。

思想：都是将并行处理的一层节点bag的相邻节点存到下一次处理的bag中。

竞争：

第 18 行的 v.dist 更新为 d+1。
幸运的是，由于都是设置为同一个值，该竞争不影响结果。
第19行，可能同时将同一个节点加入out-bag,导致额外的工作
但是这个bag数据结构是具有元素各异的性质，正好解决这个问题。
根本没有元素各异好吧。
第19行，可能同时将同一个节点加入out-bag,不会写同一个地方吗？insert

最后还是要加锁，屮。

辅助数据结构 - pennant

辅助数据结构，称为 "pennant"，是一个\(2^k\)个节点的特殊树。根只有个left子节点，该子节点有个完整是二叉树。

通过这个辅助数据结构，可以实现动态无序集的 bag 数据结构

注意，普通的k层完全二叉树，有\(\(1+2+4+2^{k-1}=2^k-1\)\)个节点。

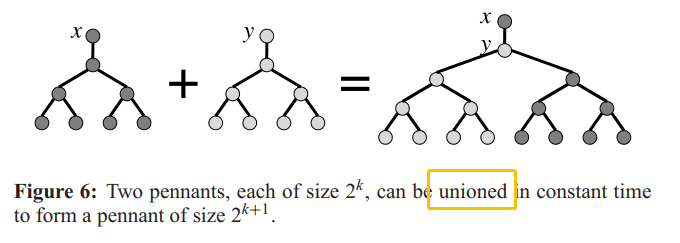
PENNANT-UNION(x,y)
   1 y. right = x. left
   2 x. left = y
   3 return x

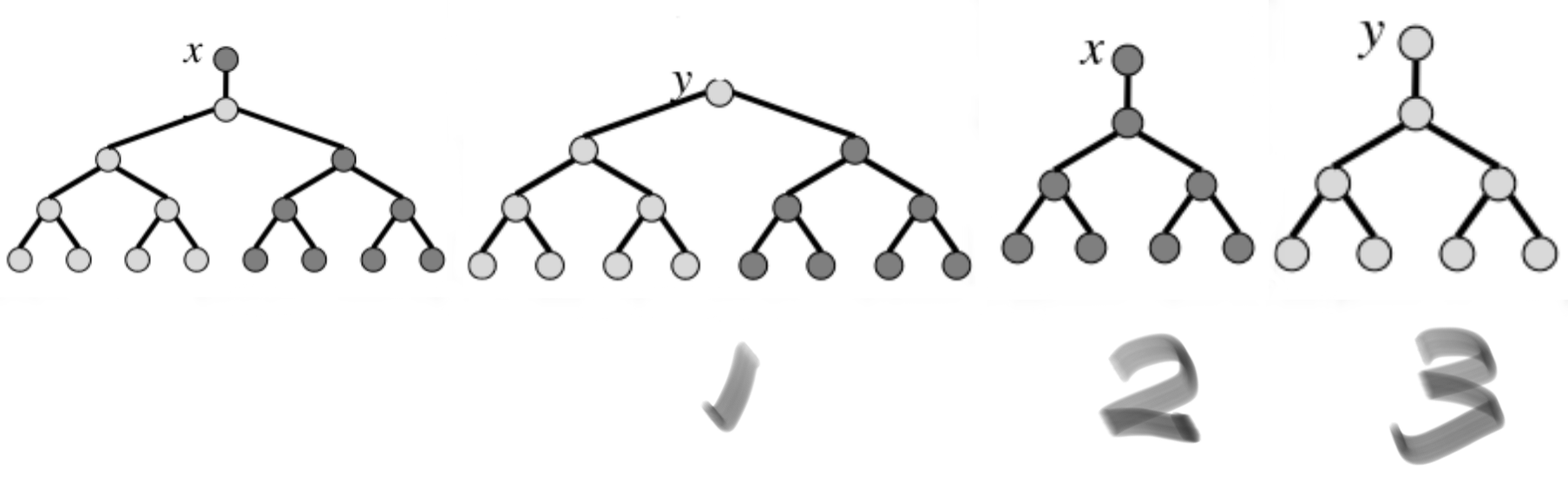
PENNANT-SPLIT(x)
   1 y = x. left
   2 x. left = y. right
   3 y. right = NULL
   4 return y

数据结构 - bags

bag是pennant的集合，其中没有相同大小的pennant。PBFS采用固定大小的数组S[0...r]称作 backbone 骨干。数组中的第k元素S[k]为空或者保存着指向大小为\(2^{k\)的pennant。可知，整个数组S[0...r]最多保存\(2}\)元素。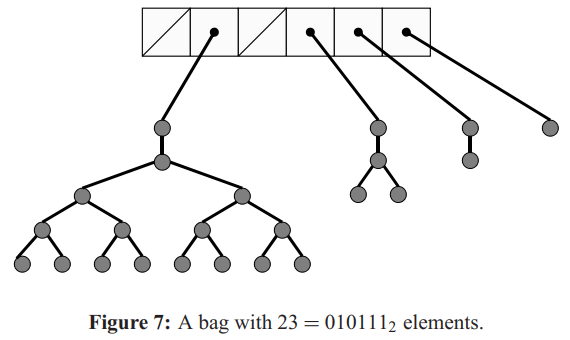所以BAG-CREATE分配了保存空指针固定大小的数组backbone,会花费Θ(r)时间。

This bound can be improved to O(1) by keeping track of the largest nonempty index in the backbone.

BAG-Insert类似二进制计数器递增的过程

BAG-INSERT(S,x)
   1 k = 0
   2 while S[k] != NULL
      3 x = PENNANT-UNION(S[k],x)
      4 S[k++] = NULL
   5 S[k] = x                 #不执行循环 S[0] = x,不是在图7这种插入。

BAG-UNION(S1,S2)     
   1 y = NULL // The “carry” bit.
   2 for k = 0 to r
   3 (S1[k],y) = FA(S1[k],S2[k],y)

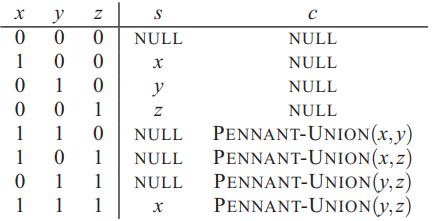
BAG-UNION(S1,S2)因为每一个PENNANT-UNION都需要固定的时间，计算FA（x，y，z）的值也需要恒定的时间。计算结果包主干中的所有条目需要Θ（r）时间。该算法可以改进为Θ（lgn），其中n是两个包中较小的包中的元素数，方法是保持每个包主干的最大非空索引，并将索引较小的包合并为索引较大的包

其中FA(x,y,z)相当于三个数的加法，c是进位，s是余位。

A Work-Efficient Parallel Breadth-First Search Algorithm (or How to Cope with the Nondeterminism of Reducers) from ACM SPAA 2010