Classical AI Models

导言

机器学习和人工智能模型算法，从一开始模仿神经元设计，到现在根据任务定制或者基于naive的思想构建(例如对抗思想、感受野、注意力机制)。模型的设计可以说是日新月异，截然不同。但是从高性能计算的角度来看，还是离不开求导操作、矩阵操作、激活函数计算这几点。剩下值得考虑的就是寻找现有或者未来模型构成计算操作的最大公约数，来对其进行特殊软硬件设计加速。或者只是对现有模型的适配加速工作。

前馈神经网络¶

前馈神经网络（Feedforward Neural Network, FNN）是一种最简单和基础的神经网络模型。它由多个神经元层（输入层、隐藏层和输出层）组成，各神经元分层排列，每个神经元只与前一层的神经元相连，接收前一层的输出，并输出给下一层。各层之间没有反馈连接。

前馈神经网络的结构和工作原理如下：

输入层：接收输入数据，每个输入值对应一个特征。
隐藏层：由多个神经元组成，接收输入层的输出并进行非线性变换，通常使用激活函数（如ReLU、Sigmoid或Tanh）。
输出层：接收隐藏层的输出并生成最终结果，输出层的神经元数目和任务有关，比如分类任务的输出层神经元数目等于类别数。

前馈神经网络的特点是数据单向流动，从输入层经过隐藏层到达输出层，没有反馈环路。这种网络通过调整权重和偏置来最小化误差函数，从而达到学习目的。常用的训练算法是反向传播算法（Backpropagation），它通过计算误差的梯度来更新权重和偏置。

前馈神经网络在许多应用中表现良好，包括分类、回归、特征提取等。然而，它也有一些局限性，如对复杂的非线性问题可能需要更深的网络结构（深度神经网络）来处理。

前馈神经网络（Feedforward Neural Network, FNN）的概念可以追溯到20世纪40年代和50年代早期神经网络研究的起步阶段。沃伦·麦卡洛克（Warren McCulloch）和沃尔特·皮茨（Walter Pitts）在1943年发表的论文中提出了神经元的数学模型，这个模型后来被认为是前馈神经网络的早期形式。

但是，前馈神经网络在现代意义上的发展要归功于20世纪80年代，尤其是1986年大卫·鲁梅尔哈特（David Rumelhart）、杰弗里·辛顿（Geoffrey Hinton）和罗纳德·威廉姆斯（Ronald Williams）在一篇论文中提出的反向传播算法（Backpropagation），这使得训练深层前馈神经网络变得可行。反向传播算法的提出和应用标志着前馈神经网络在理论和实践上的重要进展，从而推动了神经网络和深度学习的发展。

感知器¶

感知器（Perceptron）是由弗兰克·罗森布拉特（Frank Rosenblatt）在1957年提出的。感知器是最简单的FNN，没有隐藏层，只有输入层和输出层。它只能处理线性可分的问题。这一模型标志着机器学习和神经网络研究的早期阶段，尽管感知器只能解决线性可分的问题，但它为后来的神经网络研究奠定了基础。

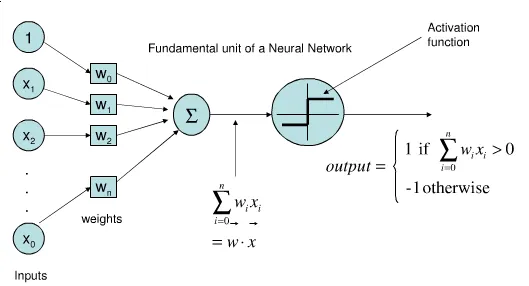
感知器由输入层、权重、偏置和输出组成，其工作原理如下：

输入层：接收外部输入的数据，每个输入值对应一个特征。
权重：每个输入特征值乘以对应的权重，权重表示该特征对输出的重要性。
加权和：将所有加权后的输入特征值相加，并加上偏置项。
激活函数：通过激活函数（通常是阶跃函数或Sigmoid函数）将加权和转换为输出值。如果加权和大于某个阈值，则输出1；否则输出0。

感知器的数学表达式为：

\[ y = f(\sum_{i=1}^n w_i x_i + b) \]

其中，\( y \) 是输出，\( f \) 是激活函数，\( w_i \) 是权重，\( x_i \) 是输入特征值，\( b \) 是偏置。

感知器可以通过调整权重和偏置来学习并分类不同的输入数据，但它只能解决线性可分的问题，对于非线性可分的问题无能为力。

多层感知器 MLP¶

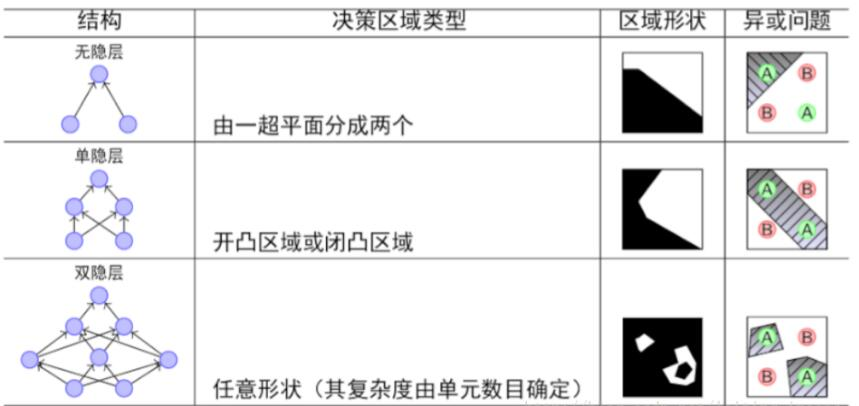
克服单层感知器局限性的有效办法就是在输入层和输出层之间引入一个或多个隐层作为输入样本的内部表示，从而将单层感知器变成多层感知器（MLP，Multilayer Perceptron）。

单隐层感知器可解决异或问题。Kolmogorov理论指出：双隐层感知器足以解决任何复杂的分类问题。[^1]

MLP可以被看作是一个有向图，由多个的节点层所组成，每一层的节点都全连接到下一层。
除了输入节点，每个节点都是一个带有非线性激活函数的神经元（或称处理单元）。
并使用反向传播算法BP的监督学习方法来训练MLP。学习过程由信号的正向传播与误差的反向传播两个过程组成。
- 正向传播时,输入样本从输入层传入,经各隐层逐层处理后,传向输出层。若输出层的实际输出与期望的输出(教师信号)不符,则转入误差的反向传播阶段。
- 反向传播时，将输出以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。

下面将详细介绍多层感知器（MLP）的前向传播和反向传播过程，包括其矩阵操作的格式，并通过一个小矩阵的示例进行解释。

前向传播¶

前向传播（Forward Propagation）是指数据从输入层传递到输出层的过程。假设我们有一个包含 \(L\) 层的神经网络，第 \(l\) 层的激活值 \( \mathbf{a}^l \) 由前一层的激活值 \( \mathbf{a}^{l-1} \) 通过权重矩阵 \( \mathbf{W}^l \) 和偏置向量 \( \mathbf{b}^l \) 计算得到。

公式如下：

\[ \mathbf{z}^l = \mathbf{W}^l \mathbf{a}^{l-1} + \mathbf{b}^l \]

\[ \mathbf{a}^l = \sigma(\mathbf{z}^l) \]

其中，\( \mathbf{z}^l \) 是第 \( l \) 层的线性组合结果， \( \sigma \) 是激活函数。

对于最后一层的输出，通常使用不同的激活函数，如分类任务中的 softmax 函数。

示例：前向传播的矩阵操作¶

假设我们有一个两层的神经网络（1个隐藏层和1个输出层），输入层有3个神经元，隐藏层有4个神经元，输出层有2个神经元。

输入层到隐藏层：

\[ \mathbf{W}^1 = \begin{pmatrix} 0.2 & 0.4 & 0.6 \\ 0.5 & 0.1 & 0.3 \\ 0.8 & 0.7 & 0.9 \\ 0.3 & 0.5 & 0.7 \end{pmatrix}, \quad \mathbf{b}^1 = \begin{pmatrix} 0.1 \\ 0.2 \\ 0.3 \\ 0.4 \end{pmatrix} \]

假设输入向量为 \( \mathbf{a}^0 = \begin{pmatrix} 1 \\ 0.5 \\ 0.3 \end{pmatrix} \)。

计算隐藏层的激活值：

\[ \mathbf{z}^1 = \mathbf{W}^1 \mathbf{a}^0 + \mathbf{b}^1 = \begin{pmatrix} 0.2 & 0.4 & 0.6 \\ 0.5 & 0.1 & 0.3 \\ 0.8 & 0.7 & 0.9 \\ 0.3 & 0.5 & 0.7 \end{pmatrix} \begin{pmatrix} 1 \\ 0.5 \\ 0.3 \end{pmatrix} + \begin{pmatrix} 0.1 \\ 0.2 \\ 0.3 \\ 0.4 \end{pmatrix} = \begin{pmatrix} 0.95 \\ 0.8 \\ 1.57 \\ 1.06 \end{pmatrix} \]

\[ \mathbf{a}^1 = \sigma(\mathbf{z}^1) \]

假设我们使用 ReLU 激活函数：

\[ \mathbf{a}^1 = \max(0, \mathbf{z}^1) = \begin{pmatrix} 0.95 \\ 0.8 \\ 1.57 \\ 1.06 \end{pmatrix} \]

隐藏层到输出层：

\[ \mathbf{W}^2 = \begin{pmatrix} 0.3 & 0.5 & 0.7 & 0.9 \\ 0.2 & 0.4 & 0.6 & 0.8 \end{pmatrix}, \quad \mathbf{b}^2 = \begin{pmatrix} 0.1 \\ 0.2 \end{pmatrix} \]

计算输出层的激活值：

\[ \mathbf{z}^2 = \mathbf{W}^2 \mathbf{a}^1 + \mathbf{b}^2 = \begin{pmatrix} 0.3 & 0.5 & 0.7 & 0.9 \\ 0.2 & 0.4 & 0.6 & 0.8 \end{pmatrix} \begin{pmatrix} 0.95 \\ 0.8 \\ 1.57 \\ 1.06 \end{pmatrix} + \begin{pmatrix} 0.1 \\ 0.2 \end{pmatrix} = \begin{pmatrix} 3.342 \\ 2.512 \end{pmatrix} \]

假设输出层使用 softmax 激活函数：

\[ \mathbf{a}^2 = \text{softmax}(\mathbf{z}^2) \]

反向传播¶

反向传播（Backpropagation）是指通过计算损失函数的梯度，逐层更新权重和偏置的过程。

损失函数的梯度计算如下：

\[ \delta^L = \nabla_a \mathcal{L} \odot \sigma'(\mathbf{z}^L) \]

\[ \delta^l = ((\mathbf{W}^{l+1})^T \delta^{l+1}) \odot \sigma'(\mathbf{z}^l) \]

其中，\( \delta^l \) 是第 \( l \) 层的误差， \( \mathcal{L} \) 是损失函数， \( \sigma' \) 是激活函数的导数。

权重和偏置的更新公式：

\[ \mathbf{W}^l = \mathbf{W}^l - \eta \delta^l (\mathbf{a}^{l-1})^T \]

\[ \mathbf{b}^l = \mathbf{b}^l - \eta \delta^l \]

其中， \( \eta \) 是学习率。

示例：反向传播的矩阵操作¶

假设我们使用均方误差（MSE）作为损失函数，并且已知输出层的实际值为 \( \mathbf{y} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \)。

计算输出层误差：

\[ \delta^2 = \mathbf{a}^2 - \mathbf{y} = \begin{pmatrix} 0.968 \\ 0.032 \end{pmatrix} - \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} -0.032 \\ 0.032 \end{pmatrix} \]

计算隐藏层误差：

\[ \delta^1 = ((\mathbf{W}^2)^T \delta^2) \odot \sigma'(\mathbf{z}^1) \]

假设 ReLU 函数的导数为 1（非负部分）：

\[ \delta^1 = \begin{pmatrix} 0.3 & 0.2 \\ 0.5 & 0.4 \\ 0.7 & 0.6 \\ 0.9 & 0.8 \end{pmatrix} \begin{pmatrix} -0.032 \\ 0.032 \end{pmatrix} \odot \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} -0.0032 \\ -0.0032 \\ -0.0032 \\ -0.0032 \end{pmatrix} \]

更新权重和偏置：

\[ \mathbf{W}^2 = \mathbf{W}^2 - \eta \delta^2 (\mathbf{a}^1)^T \]

\[ \mathbf{b}^2 = \mathbf{b}^2 - \eta \delta^2 \]

类似地：

\[ \mathbf{W}^1 = \mathbf{W}^1 - \eta \delta^1 (\mathbf{a}^0)^T \]

\[ \mathbf{b}^1 = \mathbf{b}^1 - \eta \delta^1 \]

以上就是MLP的前向传播和反向传播公式的详细解释，以及通过小矩阵的示例说明其矩阵操作。通过这些公式和操作，MLP可以进行有效的学习和优化，解决各种复杂的任务。

在多层感知器（MLP）之后，直到残差神经网络（ResNet）的发展过程中，有许多重要的神经网络架构和模型对深度学习领域产生了重大影响。以下是一些关键的网络模型，它们在不同的时间点推动了神经网络的进步：

卷积神经网络 CNN¶

卷积神经网络（CNN, Convolutional Neural Network）的出现主要受到生物学启发，特别是人类视觉系统的研究；并在图像处理领域取得了显著的成功。

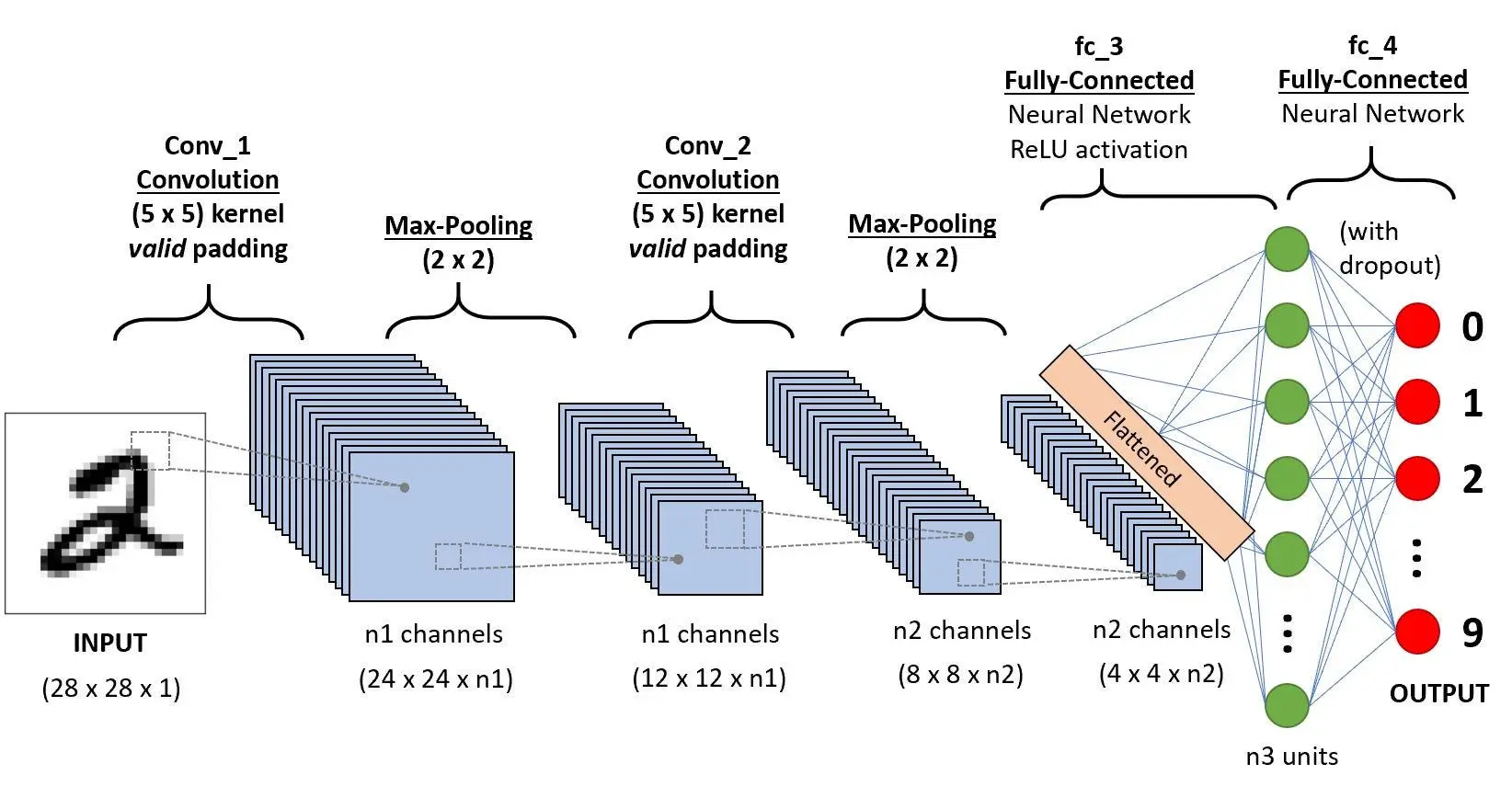
LeNet-5 (1998)：由Yann LeCun等人提出，最早用于手写数字识别任务，是第一个成功应用于实际问题的卷积神经网络。
AlexNet (2012)：由Alex Krizhevsky等人提出，首次在ImageNet竞赛中大幅度超越传统方法，使深度学习在计算机视觉领域迅速崛起。

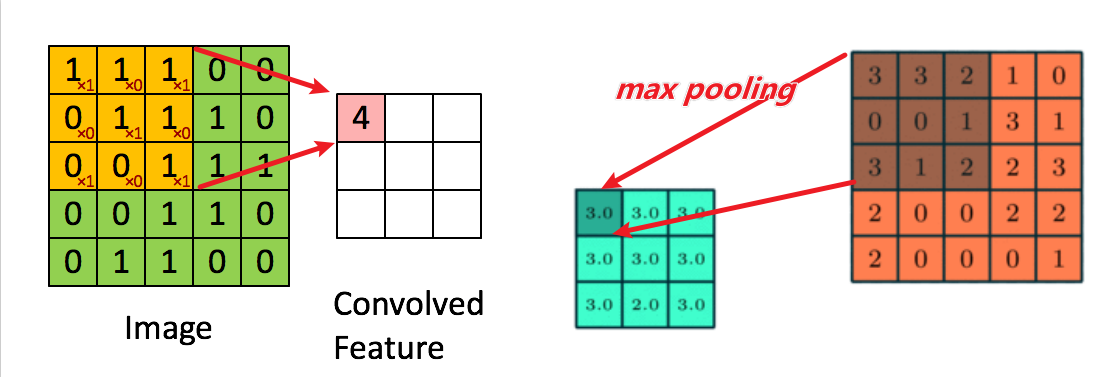
卷积神经网络由一个或多个卷积层和顶端的全连通层（对应经典的神经网络）组成，同时也包括关联权重和池化层（pooling layer）。这一结构使得卷积神经网络能够利用输入数据的二维结构。卷积可视化

深度卷积神经网络（Deep CNNs）¶

最早的卷积神经网络（如LeNet-5）通常只有几层（5-7层），包括卷积层、池化层和全连接层。
这些早期的网络结构较为简单，主要用于处理相对简单的图像分类任务（如手写数字识别）。
深度卷积神经网络的层数显著增加，常常包含几十层甚至上百层。例子包括AlexNet、VGGNet、GoogLeNet（Inception）、ResNet等。
深度网络能够捕捉更复杂、更抽象的特征，从而在更大规模、更复杂的图像数据集上表现更好。
VGGNet (2014)：由Simonyan和Zisserman提出，通过使用非常深的网络（如16或19层），展示了增加网络深度可以显著提高图像分类性能。
GoogLeNet (Inception, 2014)：由Szegedy等人提出，引入了Inception模块，通过不同尺度的卷积核进行并行计算，从而提高了网络的表达能力和计算效率。具有22层深的网络结构，但参数量较少，通过1x1卷积来减少计算量。

循环神经网络 RNN¶

循环神经网络（RNN, Recurrent Neural Network）

基础RNN (1980s)：用于处理序列数据，如时间序列和自然语言处理。
长短期记忆网络（LSTM, Long Short-Term Memory, 1997）：由Hochreiter和Schmidhuber提出，解决了基础RNN中的梯度消失和梯度爆炸问题，使得处理长序列信息变得更加有效。

如果说CNN是对空间上特征的提取， RNN则是对时序上特征的提取。

出现背景¶

循环神经网络（RNN）的出现是为了解决处理序列数据的问题。与传统的前馈神经网络（如MLP）不同，RNN具有处理时间序列数据和序列依赖的能力。RNN最早在20世纪80年代被提出，以下是其出现的关键背景和动机：

序列数据的需求：许多实际问题都涉及序列数据，如时间序列预测、自然语言处理（NLP）、语音识别等。传统的神经网络无法有效处理这些数据，因为它们不能记住序列中的上下文信息。
时间依赖关系：在很多应用中，当前的输出不仅依赖于当前的输入，还依赖于之前的输入。例如，语言中的每个单词的意义通常取决于前后的单词。
记忆能力：RNN通过循环连接使得网络具有记忆能力，可以记住前一时刻的信息，从而能够处理具有时间依赖性的任务。

RNN的模型特点¶

一般必须有编码器(将输入序列编码为一个固定长度的隐藏状态)与解码器（将编码后（Encoded）的信息解码为人类可识别的信息）

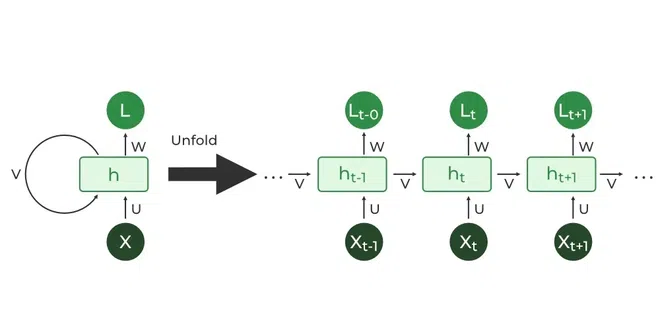
循环连接：RNN的隐藏层不仅接收当前时刻的输入，还接收上一个时刻的隐藏层状态，这使得RNN能够记住之前的状态信息。
时间步长：RNN在每个时间步长（timestep）上处理输入序列，每一步的输出依赖于当前输入和之前的隐藏状态。
权重共享：RNN在每个时间步长上使用相同的权重，这不仅减少了模型的参数数量，还确保了处理每个时间步的输入时使用相同的特征提取方法。
梯度消失和梯度爆炸问题：由于RNN在时间步长上进行反向传播，这使得梯度在多个时间步长上传播时可能会消失或爆炸，从而影响模型的训练。这也是RNN的一个主要挑战。

RNN的基本公式如下：

\[ h_t = \sigma(W_{xh} x_t + W_{hh} h_{t-1} + b_h) \]

\[ y_t = \sigma(W_{hy} h_t + b_y) \]

其中，\(h_t\) 是时间步 \(t\) 的隐藏状态，\(x_t\) 是时间步 \(t\) 的输入，\(y_t\) 是时间步 \(t\) 的输出，\(W_{xh}\), \(W_{hh}\), \(W_{hy}\) 是权重矩阵，\(b_h\), \(b_y\) 是偏置，\(\sigma\) 是激活函数（如tanh或ReLU）。

RNN擅长的领域¶

循环神经网络可以描述动态时间行为，因为和前馈神经网络（feedforward neural network）接受较特定结构的输入不同，RNN将状态在自身网络中循环传递，因此可以接受更广泛的时间序列结构输入。手写识别，语音识别和视频这些与时间有关的是最早成功利用RNN的研究结果。

自然语言处理（NLP）：RNN广泛用于文本分类、情感分析、机器翻译、文本生成、语言建模等任务。RNN能够捕捉语言序列中的上下文信息，生成连贯的文本。
语音识别：RNN可以处理语音信号的时间序列数据，将语音信号转换为文本。在语音识别系统中，RNN用于将输入的语音片段转换为对应的文本片段。
时间序列预测：在金融市场预测、天气预报、传感器数据分析等领域，RNN可以处理和预测时间序列数据的未来趋势。
视频分析：RNN可以处理视频帧序列，进行动作识别、视频分类等任务，通过分析帧与帧之间的时间依赖关系。
音乐生成：RNN可以生成连贯的音乐序列，通过学习音乐片段之间的时间依赖关系，生成新的音乐作品。

解决RNN局限性的改进模型¶

由于基本RNN存在梯度消失和梯度爆炸问题，研究人员提出了一些改进模型：

长短期记忆网络（LSTM, Long Short-Term Memory）：由Hochreiter和Schmidhuber在1997年提出，通过引入门控机制（如输入门、遗忘门和输出门），LSTM能够有效解决长期依赖问题。适合于处理和预测时间序列中间隔和延迟非常长的重要事件。
门控循环单元（GRU, Gated Recurrent Unit）：由Cho等人在2014年提出，GRU是LSTM的简化版本，具有类似的效果但计算更高效。

这些改进模型使得RNN能够更有效地处理长时间依赖关系，进一步扩展了其应用领域。

强化学习和生成对抗网络（GANs）¶

深度Q网络（DQN, Deep Q-Network, 2013-2015）：由DeepMind提出，将深度学习和强化学习结合，使得计算机能够在没有明确策略的情况下通过游戏模拟进行自我学习。
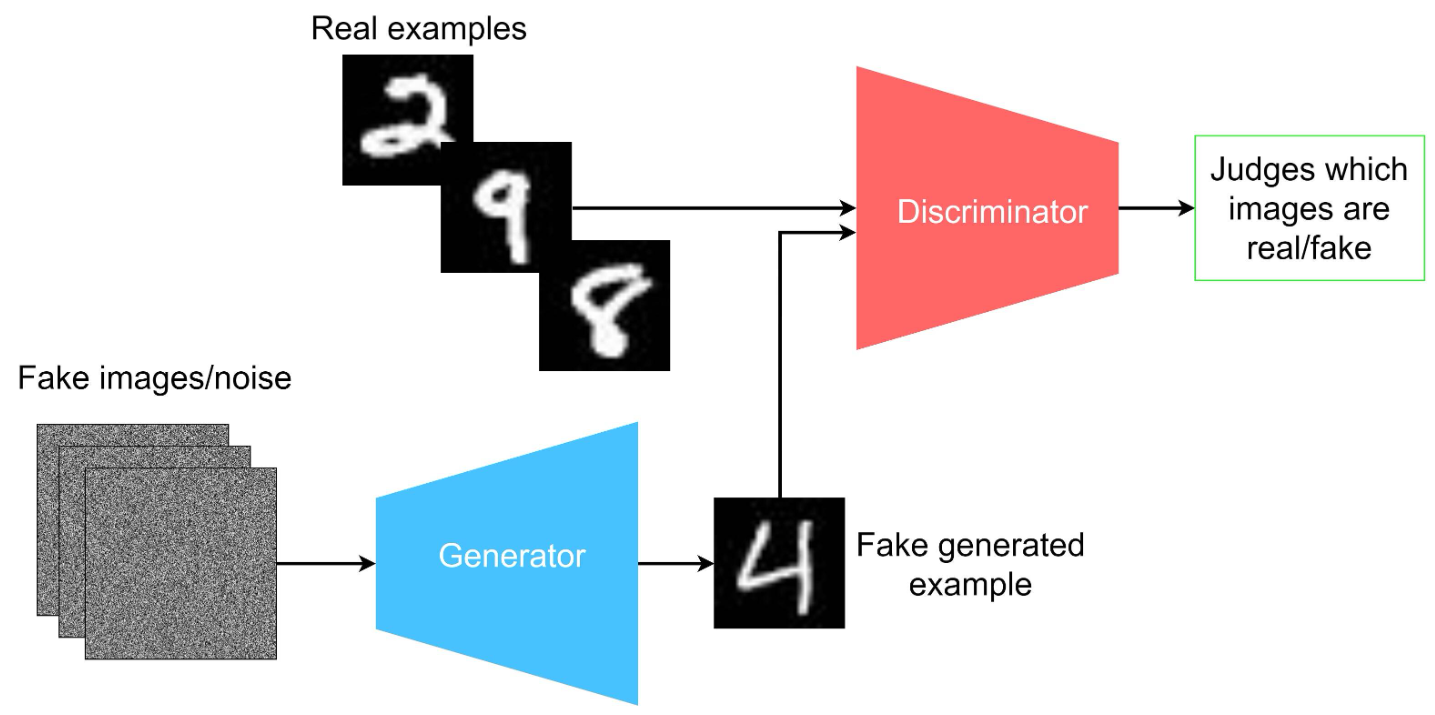
生成对抗网络（GAN, Generative Adversarial Network, 2014）：由Ian Goodfellow提出，通过对抗训练生成和判别网络，使得模型能够生成高质量的合成数据。

残差神经网络 ResNet¶

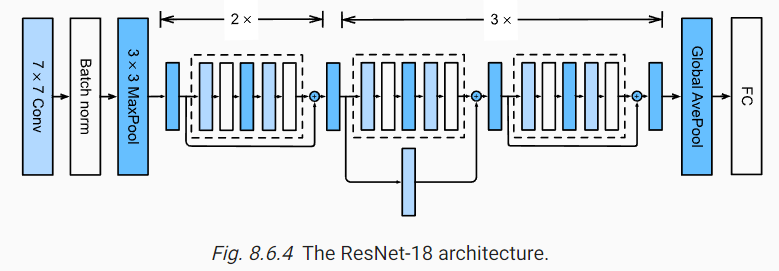
残差神经网络（Residual Neural Network，ResNet）是指一种特殊的深度神经网络结构，于2014年由Kaiming He等人提出。它属于前馈神经网络（Feedforward Neural Networks）的一种，，通过引入残差模块，解决了深度神经网络中隐藏层过多时的退化问题，使得训练非常深的网络（如50层、101层甚至更深）变得可行。这标志着神经网络训练在极大深度上的突破。

退化（degradation）问题

退化（degradation）问题是指：当网络隐藏层变多时，网络的准确度达到饱和然后急剧下降，而且这个退化不是由于过拟合引起的。而是由于网络的深度增加导致的优化问题。

退化问题的出现是由于网络深度增加后，梯度在反向传播过程中逐渐消失（梯度消失）或者变得非常大（梯度爆炸），导致网络的参数无法有效地更新，从而影响了网络的性能。这使得更深层的网络反而比较浅层的网络性能更差。

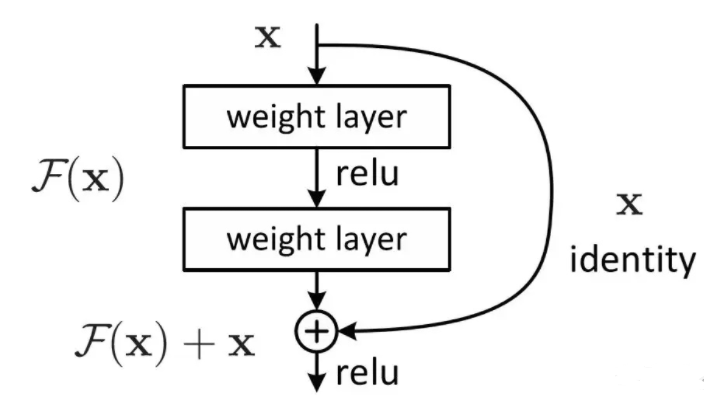
残差神经网络的主要特点是引入了跳跃连接（Skip Connection）或残差连接（Residual Connection）。跳跃连接通过将输入数据与输出数据直接相加，使得网络可以学习残差函数，即输入与期望输出之间的差异。这种结构可以解决深层神经网络训练中的梯度消失和梯度爆炸问题，有助于有效地训练更深的网络。

skip connect的思想，将输出表述为输入和输入的一个非线性变换的线性叠加，没用新的公式，没有新的理论，只是换了一种新的表达。

残差神经网络的核心思想是通过残差块(Residual Block)来构建网络层。每个残差块包含了多个卷积层和批归一化层，通过跳跃连接将输入和输出相加，并通过激活函数进行非线性变换。这样的结构可以让网络更容易地学习残差部分，从而提高网络的性能和训练效率。

注意力机制¶

注意力机制（Attention Mechanism）最早在2014年由Bahdanau等人提出，用于机器翻译任务。初始idea是输入信息是有重要程度的区分的，需要不同程度的引起模型的“注意”。其核心思想是，在处理序列数据时，当前时间片的输出可能仅更注重原句子的某几个单词而不是整个句子, 可以动态地关注输入序列的不同部分，从而提高模型的性能。通过Attention机制，模型可以同时学习原句子和目标句子的对齐关系和翻译关系。

基本概念¶

注意力机制的核心是计算注意力权重，这些权重用于衡量输入序列中每个元素的重要性。一般来说，注意力机制可以分为三个步骤：

计算注意力权重：
- 对于每个输入元素，计算其与当前输出的相似度得分。通常使用点积、加法等方式来计算。
- 将这些得分进行归一化，通常使用softmax函数，使得权重和为1。
加权求和：
- 将输入序列中的每个元素与对应的注意力权重相乘，然后将这些加权后的元素进行求和，得到最终的上下文向量。
生成输出：
- 使用上下文向量和当前输出状态一起生成最终的输出。

数学表达如下：

\[ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V \]

其中，\( Q \) 是查询向量（query），\( K \) 是键向量（key），\( V \) 是值向量（value），\( d_k \) 是键向量的维度，用于缩放。

相对于RNN的优势¶

并行化：
- RNN在处理序列数据时是逐步进行的，时间片 t 的计算依赖 t-1 时刻的计算结果, 这限制了并行计算的能力。
- 注意力机制可以在计算时并行处理输入序列中的所有元素，大大提高了计算效率。
长程依赖：
- RNN在处理长序列时容易出现梯度消失或梯度爆炸问题，使得模型难以捕捉到长程依赖关系。
- 注意力机制通过计算所有输入元素的加权和，可以直接捕捉到长程依赖关系，不受序列长度的影响。
灵活性：
- RNN的结构相对固定，处理不同类型的输入和输出需要特定的设计。
- 注意力机制的设计非常灵活，可以很容易地应用于不同的任务，如机器翻译、文本生成、图像处理等。
可解释性：
- RNN的内部状态和输出难以解释和理解。
- 注意力机制的注意力权重可以直观地展示模型关注输入序列的哪些部分，从而提高模型的可解释性。

自注意力机制（Self-Attention）¶

自注意力机制是注意力机制的一种特殊形式，主要用于处理输入序列中的元素之间的关系。在自注意力机制中，查询、键和值向量都来源于同一输入序列。

自注意力机制的一个重要应用是Transformer模型。Transformer模型完全基于自注意力机制，摒弃了RNN的结构，在机器翻译、文本生成等任务中取得了显著的成功。其结构如下：

编码器（Encoder）：由多个自注意力层和前馈神经网络组成，用于编码输入序列。
解码器（Decoder）：由多个自注意力层、编码器-解码器注意力层和前馈神经网络组成，用于生成输出序列。

总结¶

注意力机制 提供了一种灵活、并行化和可解释的方法来处理序列数据，克服了RNN在处理长程依赖和计算效率上的局限。
自注意力机制 和 Transformer 模型在自然语言处理和其他任务中取得了巨大的成功，推动了深度学习领域的进一步发展。

Transformer模型¶

Transformer模型是由Vaswani等人在2017年提出的，是一种完全基于注意力机制的深度学习模型，最初应用于机器翻译任务。与传统的循环神经网络（RNN）和卷积神经网络（CNN）不同，Transformer模型完全抛弃了循环和卷积结构，而是通过自注意力机制（Self-Attention）来捕捉序列数据中的依赖关系。

核心内容¶

Transformer模型的核心包括两个部分：编码器（Encoder）和解码器（Decoder）。每个部分由多个层（Layer）堆叠而成。一个典型的Transformer由6层编码器和6层解码器组成，总共12层的Encoder-Decoder。

1. 编码器（Encoder）¶

每个编码器层包含两个子层：

多头自注意力机制（Multi-Head Self-Attention）：通过多个头（head）并行计算自注意力，捕捉不同子空间的特征。
前馈神经网络（Feed-Forward Neural Network, FFN）：通过两个线性变换和一个激活函数（通常是ReLU）进行非线性映射。

每个子层后都进行层归一化（Layer Normalization）和残差连接（Residual Connection），使得网络更容易训练。

2. 解码器（Decoder）¶

每个解码器层包含三个子层：

多头自注意力机制（Multi-Head Self-Attention）：类似于编码器，但在解码过程中，当前位置只关注前面的位置信息。
编码器-解码器注意力机制（Encoder-Decoder Attention）：解码器的每个位置通过注意力机制关注编码器的输出。
前馈神经网络（Feed-Forward Neural Network, FFN）：与编码器相同。

每个子层同样进行层归一化（Layer Normalization）和残差连接（Residual Connection）。

注意力掩码（Attention Masking）¶

注意力掩码机制是Transformer模型中处理变长序列和自回归任务的重要手段，通过填充掩码和因果掩码确保模型能够正确地处理填充部分并防止信息泄露，从而提高模型的泛化能力和性能。

在Transformer模型中，注意力掩码用于处理以下两个主要问题：

填充标记（ tokens）：
当处理变长序列时，需要将所有序列填充（padding）到相同长度。填充标记（）本身不含有实际信息，因此模型在计算注意力权重时应该忽略这些填充部分。
因果注意力（Causal Attention）：
在解码过程中，为了防止模型在预测下一个单词时看到未来的信息，需要对未来的位置进行掩码处理，确保模型只能看到当前和之前的位置。这种机制也称为“自回归”注意力。

如何实现注意力掩码

填充掩码（Padding Mask）

在计算注意力权重之前，填充掩码被应用到注意力得分上，将填充位置的得分设为负无穷，确保这些位置在计算softmax时得到的注意力权重接近于零。

假设输入序列的长度为 \( T \)，填充掩码可以表示为一个 \( T \times T \) 的矩阵，其中填充值对应的位置为1，其余位置为0。

因果掩码（Causal Mask）

因果掩码确保每个位置只能看到当前位置之前的位置（包括当前的位置），防止信息泄露。对于长度为 \( T \) 的序列，因果掩码是一个上三角矩阵，其上三角部分（不包括对角线）为负无穷，其余部分为0。

注意力计算中的应用

在计算自注意力时，首先计算注意力得分矩阵 \( \mathbf{S} = \frac{\mathbf{QK}^T}{\sqrt{d_k}} \)，然后应用掩码：

\[ \mathbf{S}_{\text{masked}} = \mathbf{S} + \text{mask} \]

接着，使用softmax函数计算注意力权重：

\[ \mathbf{A} = \text{softmax}(\mathbf{S}_{\text{masked}}) \]

最后，计算加权和，得到上下文向量：

\[ \text{Attention}(Q, K, V) = \mathbf{A} \mathbf{V} \]

示例

假设我们有一个批次（batch）包含两个序列，长度分别为4和3，填充到相同长度4：

序列1: [x1, x2, x3, x4]
序列2: [y1, y2, y3, <pad>]

填充掩码为：

[[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 1]]  // <pad>位置为1，其余位置为0

因果掩码为：

[[0, -∞, -∞, -∞],
[0, 0, -∞, -∞],
[0, 0, 0, -∞],
[0, 0, 0, 0]]

Transformer的优势¶

并行计算：
- Transformer模型完全抛弃了循环结构，使得序列中的所有位置可以并行计算，大大提高了训练效率。
捕捉长程依赖：
- 自注意力机制能够直接关注输入序列中的所有位置，不受序列长度的限制，能够有效捕捉长程依赖关系。
灵活性：
- Transformer模型可以很容易地扩展和修改，适用于各种任务，如机器翻译、文本生成、语音识别等。
性能优越：
- 在多个自然语言处理任务中，Transformer模型（如BERT、GPT等）取得了显著的性能提升，成为当前最先进的模型之一。

有待改进的地方¶

计算资源需求：
- Transformer模型的自注意力机制需要计算序列中所有位置之间的关系，计算复杂度为 \(O(n^2)\)，对于长序列数据，计算和存储需求非常高。
长序列处理：
- 虽然自注意力机制能够捕捉长程依赖，但处理非常长的序列时，计算复杂度和内存占用仍然是一个瓶颈。
- 为此，提出了一些改进方法，如Transformer-XL、Longformer、Linformer等，旨在提高处理长序列的效率。
数据需求：
- Transformer模型通常需要大量的训练数据才能表现良好，对于数据量较少的任务，模型可能会表现不佳。
解释性：
- 尽管注意力机制提供了一定的可解释性，但整个Transformer模型仍然是一个复杂的黑箱，对于某些任务，理解模型的决策过程仍然具有挑战性。

总结¶

Transformer模型通过自注意力机制实现了并行计算和高效的长程依赖捕捉，极大地提高了自然语言处理任务的性能。然而，其高计算和存储需求、对长序列的处理能力、数据需求和模型解释性等方面仍有待进一步改进。尽管如此，Transformer已经成为深度学习领域的一大突破，推动了自然语言处理和其他相关领域的发展。

Bert（自编码模型）¶

谷歌团队提出的用于生成词向量的BERT算法的最重要的部分便是本文中提出的Transformer的概念。

BERT的全称是Bidirectional Encoder Representation from Transformers，就是双向Transformer的Encoder。

BERT还有一点很重要，它将CV里的预训练引入了NLP问题中，使得其余的NLP任务可以在其预训练集上进一步训练，或者拿来直接用。

ELMO¶

ELMO的全称是Embedding from Language Models。就ELMO模型本身的训练过程来说，它通过一个两层的双向LSTM，使用语言模型训练，也就是说利用一句话的上文Context-Before和下文Context-After来预测当前词。

Large Vision Model¶

SegGPT ？ InPainting? 师兄的介绍

港中文128页全球首份Gemini vs GPT-4V多模态PK报告

参考文献¶

漫谈ANN(2)：BP神经网络 ↩