Dynamic Programming
动态规划简介¶
将一件事情分成若干阶段,然后通过阶段之间的转移达到目标。由于转移的方向通常是多个,因此这个时候就需要决策选择具体哪一个转移方向。
动态规划所要解决的事情通常是完成一个具体的目标,而这个目标往往是最优解。并且:
- 阶段之间可以进行转移,这叫做动态。
- 达到一个可行解(目标阶段) 需要不断地转移,那如何转移才能达到最优解?这叫规划。
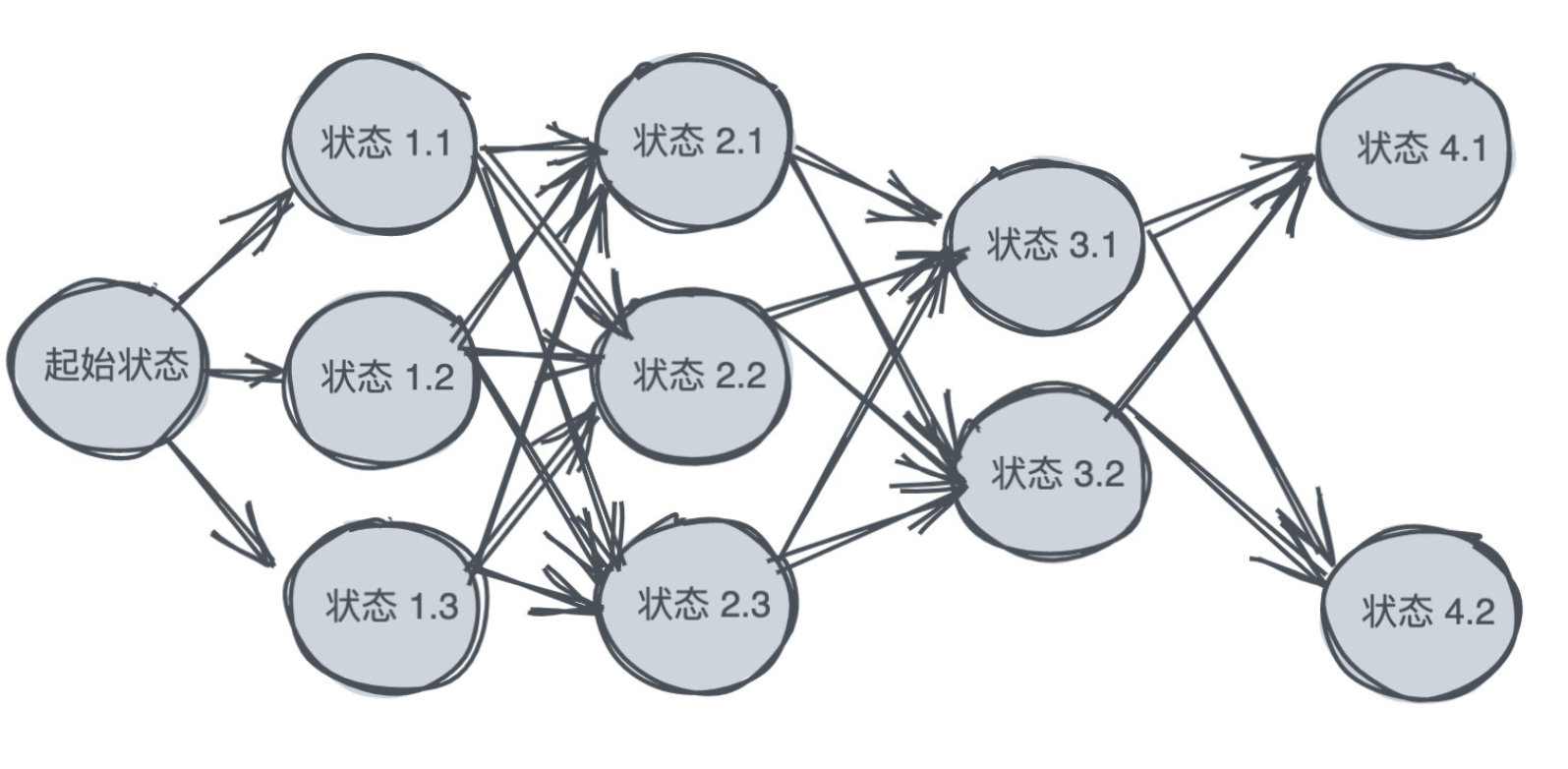
每个阶段抽象为状态(用圆圈来表示),状态之间可能会发生转化(用箭头表示)。可以画出类似如下的图:
性质:
- 最优子结构
- 问题的最优解所包含的子问题的解也是最优的
- 注意: 具有最优子结构也可能是适合用贪心的方法求解。
- 无后效性
- 已经求解的子问题,不会再受到后续(父问题)决策的影响。
- 即子问题的解一旦确定,就不再改变,不受在这之后、包含它的问题的求解决策的影响。
- 子问题重叠
- 如果有大量的重叠子问题,我们可以用空间将这些子问题的解存储下来,避免重复求解相同的子问题,从而提升效率。
基本思路¶
对于一个能用动态规划解决的问题,一般采用如下思路解决:
- 将原问题划分为若干 阶段,每个阶段对应若干个子问题,提取这些子问题的特征(称之为 状态);
- 寻找每一个状态的可能 决策,或者说是各状态间的相互转移方式(用数学的语言描述就是 状态转移方程)。
- 按顺序求解每一个阶段的问题。 如果用图论的思想理解,我们建立一个 有向无环图,每个状态对应图上一个节点,决策对应节点间的连边。
难点,重点¶
如何找到转移关系:
- 可以伸缩的维度: 一般是数组的下标,或者是字符串的下标,或者是树的节点。也可以是问题的query数值。
- 分情况讨论的,最大值为不同情况的最大值。方案数为所有情况的总和。
DP分类¶
- 背包DP
- 0-1背包
- 定义:每个物体只有两种可能的状态(取与不取),对应二进制中的 0 和 1,这类问题便被称为「0-1 背包问题」
- 一般有个总cost为W来限制选择
- 基础版:可以通过滚动数组减少空间占用,但是注意遍历方向
- 常见变形:
- 至多装capacity,求方案数/最大价值和
- 恰好装capacity,求方案数/最大/最小价值和
- 至少装capacity,求方案数/最小价值和
- 变种:总cost等于W时,和为half的子集是否存在
- 方法一:
- 背包的体积为sum / 2
- 每个物品 cost = value
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 方法二:
- 状态:前i个元素,和为j的子集是否存在
- 转移关系: \( f(i,j)=(f(i-1,j)+f(i-1,j-a[i])>0)?1:0 \) 注意:
f[i,0]=1
- 变种:选择和为k的子集的
- 变种2:总cost等于W时,和为half的子集的个数 题目:2022.9.23-求和
- 状态:前i个元素,和为j的子集个数
- 转移关系: \( f(i,j)=f(i-1,j)+f(i-1,j-a[i]) \) 注意:
f[i,0]=1
- 完全背包: 每个物体可以选择多次
- 转移关系: 也可以由f(i, j-w)转移到f(i,j)
-
多重背包: 每个物体可以选择\( k_i \)次
- 朴素思路: 每步可以总\( k_i \)里选最大, \( f_{i,j} = max_{k=0}^{k_i}(f_{i-1,j - k \times w_{i}} + v_{i} \times k ) \)
- 二进制分组优化
- 思想:多重背包,其实是有很多重复元素的0-1背包,通过二进制来唯一表示选取,来最小0-1背包的可选物品数
- 具体操作: 方法是:将第 i 种物品分成若干件物品,其中每件物品有一个系数,这件物品的费用和价值均是原来的费用和价值乘以这个系数。使这些系数分别为\( 1,2,4,\ldots,2{k-1},n-2k+1 \),且 k 是满足\( n[i]-2^k+1>0 \)的最大整数。例如,如果
n[i]为 13,就将这种物品分成系数分别为 1, 2, 4, 6 的 4 件物品。 - 效果:将第 i 种物品分成了 O(logn[i]) 种物品,将原问题\( O(V\times\sum n[i]) \)转化为了复杂度为\( O(V\times\sum \log n[i]) \)的 01 背包问题
int num[maxn][2], dp[maxn]; int N, V, c, w, n, tot; memset(dp, 0, sizeof dp); cin >> V >> N; tot = 1; for(int i = 1; i <= N; ++i) { cin >> c >> w >> n; // 第 i 物品的费用、价值和数量 for(int k = 1; k < n; k<<=1)//左移求下一个所需二进制数 { num[tot][0] = k*c; // 添加 子物品 num[tot++][1] = k*w; n -= k; } num[tot][0] = n*c; // 添加n[i]-2^k+1的 子物品 num[tot++][1] = n*w; } for(int i = 1; i < tot; ++i) { for(int j = V; j >= num[i][0]; --j) // 0-1 背包 滚动数组实现 dp[j] = max(dp[j], dp[j-num[i][0]]+num[i][1]); } - 单调队列优化 to finish
-
区间DP
- \( f(i,j)=max_k{f(i,k)+f(k+1,j)+cost} \)
- DAG 上的DP
- DAG(Directed Acyclic Graph) 即 有向无环图,一些实际问题中的二元关系都可使用 DAG 来建模,从而将这些问题转化为 DAG 上的最长(短)路问题。
- to do
- 树形 DP 往往需要递归DFS
- 分阶段参数:当前子树的根节点
- 转移关系:当前子树的根节点和其子节点的关系
- 例题: to do
记忆化搜索¶
- 子问题间重叠的部分会有很多,同一个子问题可能会被重复访问多次,效率还是不高。
- 思路: 记忆化,参数一定,那么返回值也一定不会变,因此下次如果碰到相同的参数,我们就可以将上次计算过的值直接返回,而不必重新计算。这样节省的时间就等价于去除的重叠子问题的耗时。
- 解决方法:把每个子问题的解存储下来,通过记忆化的方式,确保每个子问题只被计算一次。
如何写记忆化搜索¶
- 方法一
- 把这道题的 dp 状态和方程写出来
- 根据它们写出 dfs 函数
- 添加记忆化数组
- 方法二
- 写出这道题的暴搜程序(最好是 dfs)
- 将这个 dfs 改成「无需外部变量」的 dfs
- 添加记忆化数组
实例:朴素DFS递归,实现记忆化¶
爬楼梯问题的暴力普通递归DFS代码
function climbStairs(n) {
if (n === 1) return 1;
if (n === 2) return 2;
return climbStairs(n - 1) + climbStairs(n - 2);
}
memo = {}
def climbStairs(n):
if n == 1:return 1
if n == 2: return 2
if n in memo: return memo[n]
ans = func(n - 1) + func(n-2)
memo[n] = ans
return ans
climbStairs(10)
优化技巧¶
状态压缩 & 动态规划¶
状压+动态规划(DP, Dynamic Programming)
使用的数有限(共 10 个),并且使用到的数最多出现一次,容易想到使用「状压 DP」来求解:我们使用一个二进制数来表示具体的子集具体方案。
定义 f[state] 为当前子集选择数的状态为 state 时的方案数,state 为一个长度 10 的二进制数,若 state 中的第 k 位二进制表示为 1,代表数值 p[k] 在好子集中出现过;若第 k 位二进制表示为 0 代表 p[k] 在好子集中没出现过。
状态压缩¶
状态压缩有关,比如用 4 个字节存储状态
需要进一步的研究学习¶
动态规划 与 np完全的关系
遇到的问题¶
暂无
开题缘由、总结、反思、吐槽~~¶
参考文献¶
视频: https://www.bilibili.com/video/BV1Xj411K7oF/?vd_source=5bbdecb1838c6f684e0b823d0d4f6db3
https://oi-wiki.org/dp/basic/
https://www.zhihu.com/question/316416327/answer/626807333