Flood fill Algorithm
算法介绍¶
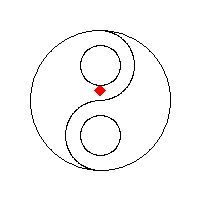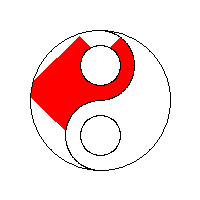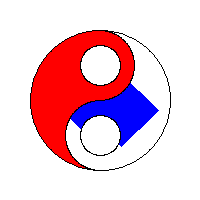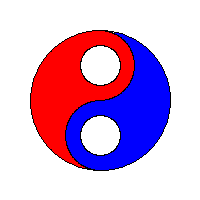
泛洪算法——Flood Fill，（也称为种子填充——Seed Fill，其中基于栈/队列的显式实现（有时称为“Forest Fire算法”））是一种算法，用于确定连接到多维数组中给定节点的区域。用于填充具有不同颜色的连接的，颜色相似的区域。泛洪算法的基本原理就是从一个像素点出发，以此向周边的像素点扩充着色，直到图形的边界。
算法参数及特点¶
参数：
- 起始节点（start node）
- 目标颜色（target color）
- 替换颜色（replacement color）
数据结构：
明确地或隐式地使用队列或堆栈数据结构。
常见实现¶
四邻域泛洪¶
将像素点(x,y)周围的上下左右四个点分别进行着色。
八邻域泛洪¶
将一个像素点的上下左右，左上，左下，右上，右下都进行着色。
描绘线算法(Scanline Fill)¶
（我感觉就是满足访存局部性原理，然后就快一些
void floodFillScanline(int x, int y, int newColor, int oldColor){
if(newColor==oldColor) return;
if(screen[x][y]!=oldColor) return;
emptyStack();
int x1;
bool spanAbove, spanBelow;
if(!push(x,y)) return;
while(pop(x,y)){
x1=x;
while(x1>0&&screen[x1][y]==oldColor) x1--;
x1++;
spanAbove = spanBelow = 0;
while(x1<w&&screen[x1][y]==oldColor){
screen[x1][y]=newColor;
if(!spanAbove&&y>0&&screen[x1][y-1]==oldColor){ //这里判断出了上行的元素可以被染色，可能为了修改screen的访存连续性，所以这里没修改。而且你改了上行的值，却没考虑其四周，会有完备性的问题。
if(!push(x1,y-1)) return;
spanAbove=1;
}
else if(spanAbove&&y>0&&screen[x1][y-1]!=oldColor){
spanAbove=0; //不压入重复过多的元素
}
if(!spanBelow&&y<h-1&&screen[x1][y+1]==oldColor){
if(!push(x1,y+1)) return;
spanBelow=1;
}
else if(spanBelow&&y<h-1&&screen[x1][y+1]!=oldColor){
spanBelow=0;
}
x1++;
}
}
}
但是程序是上下行同时入栈/队列，写成两个，先pop一个，访存更好。
描绘线算法(Scanline Fill)的并行实现¶
直接将push变成用新线程重新调用程序task。
讨论数据冲突(IPCC)¶
每行各自修改自己行screen，不会冲突。 访问隔壁行screen，但是只在意oldColor，对是否染色不关心。？
记录修改过的数据，是每个线程每行中的连续一个范围，index1~index2。由于每个线程的任务变成每行，任务量多了，这里加个锁，应该不会影响性能，维护一个行数大小的数组，每个元素存每行被标记的index,要不要有序呢?这主要看cache页能不能存下一行。然后后面还原就可以对每行omp,保证访存连续性。但这不是最优的，详见ipcc10总结。
大规模行为（Large-scale behaviour）¶
以数据为中心（data-centric）¶
小并行，每个像素一次检查4个或者8个
以流程为中心（process-centric）¶
使用堆栈。使用邻接技术和堆栈作为其种子像素存储的4路泛洪填充算法产生具有“后续填充的间隙”行为的线性填充。 这种方法尤其适用于较旧的8位计算机游戏。
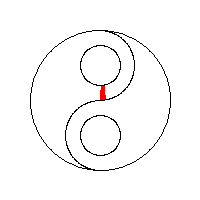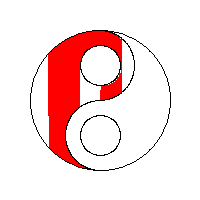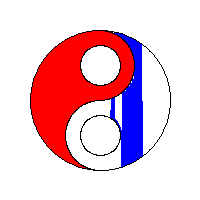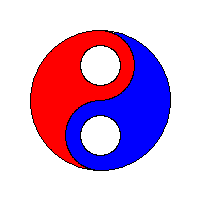
需要进一步的研究学习¶
最后的以流程为中心方法没懂，怎么实现
并行BFS(广度优先搜索)
遇到的问题¶
暂无
开题缘由、总结、反思、吐槽~~¶
IPCC 初赛 EnforceLabelConnectivity函数需要改成并行的图填充算法
参考文献¶
https://www.pianshen.com/article/172962944/